题目内容
P(1,1)为椭圆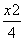 +
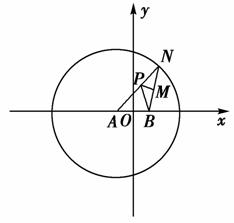
+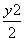 =1内的一定点,过P点引一弦,与椭圆相交于A、B两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度.
=1内的一定点,过P点引一弦,与椭圆相交于A、B两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度.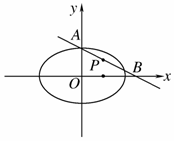
设弦AB所在的直线方程为
y-1=k(x-1),A、B两点坐标分别为
(x1,y1),(x2,y2),则
x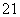 +2y
+2y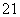 =4,① x
=4,① x +2y
+2y =4.②
=4.②
①-②得:
(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0.
∵P(1,1)为弦AB的中点,∴x1+x2=2,y1+y2=2.
∴k= =-
=-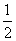 .
.
∴所求直线的方程为y-1=-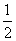 (x-1).
(x-1).
即x+2y-3=0.
将其代入椭圆方程整理得,6y2-12y+5=0.
根据弦长公式,有
|AB|= =
= .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 满足
满足 ,设
,设 是方程
是方程 的两根,则
的两根,则 的取值范围是 。
的取值范围是 。 =1的交点为A、B,点P为椭圆上的动点,则使△PAB的面积为
=1的交点为A、B,点P为椭圆上的动点,则使△PAB的面积为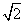 -1的点P的个数为________.
-1的点P的个数为________.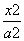 +
+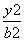 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为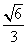 ,椭圆短轴的一个端点与两个焦点构在的三角形的面积为
,椭圆短轴的一个端点与两个焦点构在的三角形的面积为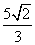 .
.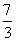 ,0),求证:
,0),求证: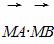 为定值.
为定值.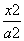 -
-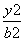 =1(a>0,b>0)的渐近线方程为y=±
=1(a>0,b>0)的渐近线方程为y=±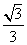 x,若顶点到渐近线的距离为1,则双曲线的方程为( )
x,若顶点到渐近线的距离为1,则双曲线的方程为( )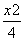 -
-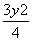 =1 B.
=1 B.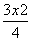 -
-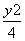 =1
=1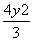 =1
=1 -
- =1的离心率e=2,则m=________.
=1的离心率e=2,则m=________.
 D.
D.
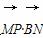 =0.
=0.