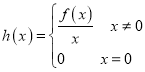Question

【题目】设集合，如果对于的每一个含有个元素的子集，中必有个元素的和等于，称正整数为集合的一个“相关数”

（1）当时，判断和是否为集合的“相关数”，说明理由；

（2）若为集合的“相关数”，证明：.

Answer 1

【答案】（1）5不是集合的“相关数”，6是集合的“相关数”；（2）证明见解析.

【解析】

（1）写出，分别考虑含有5个元素的子集和含有6个元素的子集讨论其中某四个数之和是否为13即可；

（2）分析的含有个元素的集合，，其中任意四个元素之和的最小值，不可能等于，所以不是集合的“相关数”，分析当时，不是集合的“相关数”，即可得证.

（1）当时，，

它的5个元素的子集中，

它的四个元素之和的最小值，其中任意四个元素之和都不可能为13，所以5不是集合的“相关数”，

它的6个元素的子集中只能是，存在四个元素，所以6是集合的“相关数”；

（2）若为集合的“相关数”，假设，则，

分析的含有个元素的集合，其中任意四个元素之和的最小值，不可能等于，则不是集合的“相关数”，与题矛盾，

所以，即.