题目内容

已知f（x）在R上为减函数，若f（7x2）＞f（20x+3），则实数x的取值范围是
 
．
考点：函数单调性的性质
专题：函数的性质及应用
分析：由题意可得7x2 ＜20x+3，由此求得x的范围．
解答： 解：根据f（x）在R上为减函数，若f（7x2）＞f（20x+3），
可得7x2 ＜20x+3，求得-
1
7
＜x＜3，
故答案为：（-
1
7
，3）．
点评：本题主要考查函数的单调性的性质，体现了等价转化的数学思想，属于基础题．
练习册系列答案
相关题目
求值：
33+8
2
+
33-8
2
．
求下列函数定义域：
（1）f（x）=
5
|x|-3
-x；
（2）y=
x-1+
1-x
．
求方程
13-
13+x
=x的实数解．
设函数f（x）=2|x+1|-|x-1|，求使f（x）≥2
2
的x的取值范围．
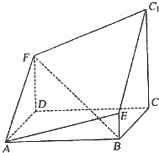如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，BC=2，CC1=3，BE=1
（Ⅰ）求BF的长；
（Ⅱ）求面AEC1F与底面ABCD所成二面角的余弦值
（Ⅲ）求点C到平面AEC1F的距离．
数列{an}的前n项和为Sn，S3=6a1，且对n∈N*，点（n，an）恒在直线f（x）=2x+k上，其中k为常数．
（1）求数列{an}的通项公式；
（2）记Tn=
1
S1
+
1
S2
+
1
S3
+…+
1
Sn
，求T20的值．
分析说明下列对应是否为A到B的函数：A=[0，2]，B=[0，4]，f取x和x2中的最小值．
方程x2+3（y-1）2=9的曲线关于（　　）对称．
A、x轴B、y轴
C、原点D、以上都不对

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网