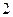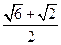题目内容
半径为
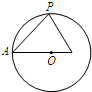
的球内有一个内接正三棱锥P-ABC,过球心O及一侧棱PA作截面截三棱锥及球面,所得截面如右图所示,则此三棱锥的侧面积为______.
| 3 |

如图球的截面图就是正三棱锥中的△PAD,
已知半径为
的球,
所以AO=PO=
,且PO⊥AO
所以侧棱长PA=
,
AD=
AO=
,AB=
,AB=3,
截面PAB面积是:
×AB×
=
∴则此三棱锥的侧面积为
故答案为:

已知半径为
| 3 |
所以AO=PO=
| 3 |
所以侧棱长PA=
| 6 |
AD=
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
截面PAB面积是:
| 1 |
| 2 |
PA2-(
|
| 3 |
| 4 |
| 15 |
∴则此三棱锥的侧面积为
| 9 |
| 4 |
| 15 |
故答案为:
| 9 |
| 4 |
| 15 |


练习册系列答案
相关题目




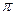 ,则球的体积为________;
,则球的体积为________; 中,平面
中,平面 平面
平面 ,
, ,
, 是等边三角形,已知
是等边三角形,已知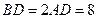 ,
, .
. (Ⅰ)设
(Ⅰ)设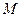 是
是 上的一点,证明:平面
上的一点,证明:平面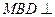 平面
平面 ;
; 的面对角线
的面对角线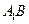 上存在
上存在 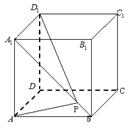 一点
一点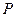 使得
使得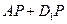 取得最小值,则此最小值为
取得最小值,则此最小值为