题目内容
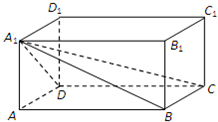
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a(a为常数).
(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B-CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
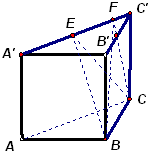
(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B-CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.

(Ⅰ)取AC中点D,连接BD.
∵AB=BC,∴△ABC为等腰三角形,D为底边AC中点,∴BD⊥AC.
∵ABC-A′B′C′是直三棱柱,∴AA′⊥平面ABC,
∵BD?平面ABC,∴BD⊥AA′.
又AA′∩AC=A,∴直线BD⊥平面ACC′A′.
∵CE?平面ACC′A′,∴BD⊥CE
∴直线BD即为所求.------(5分)
(Ⅱ)∵ABC-A′B′C′是直三棱柱,
∴CC′⊥平面A′B′C′,
∵EF?平面A′B′C′,∴CC′⊥EF
∴△CEF的边EF上的高为线段CC′,
由已知条件得CC′=AA′=1,且EF=a(常数),
故△CEF的面积S=
EF•CC′=
a
由(Ⅰ)可知,BD⊥平面ACC′A′,故BD为三棱锥B-CEF的高.
在等腰三角形ABC中,可求得BD=
,
∴三棱锥B-CEF的体积V=
S•BD=
a为定值.------(10分)
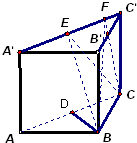
∵AB=BC,∴△ABC为等腰三角形,D为底边AC中点,∴BD⊥AC.
∵ABC-A′B′C′是直三棱柱,∴AA′⊥平面ABC,
∵BD?平面ABC,∴BD⊥AA′.
又AA′∩AC=A,∴直线BD⊥平面ACC′A′.
∵CE?平面ACC′A′,∴BD⊥CE
∴直线BD即为所求.------(5分)
(Ⅱ)∵ABC-A′B′C′是直三棱柱,
∴CC′⊥平面A′B′C′,
∵EF?平面A′B′C′,∴CC′⊥EF
∴△CEF的边EF上的高为线段CC′,
由已知条件得CC′=AA′=1,且EF=a(常数),
故△CEF的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
由(Ⅰ)可知,BD⊥平面ACC′A′,故BD为三棱锥B-CEF的高.
在等腰三角形ABC中,可求得BD=
| ||
| 2 |
∴三棱锥B-CEF的体积V=
| 1 |
| 3 |
| ||
| 12 |


练习册系列答案
相关题目
 π
π π
π π
π

 厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高
厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高