题目内容
如图,在四棱锥 中,平面
中,平面 平面
平面 ,
, ,
,
 是等边三角形,已知
是等边三角形,已知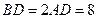 ,
, .
.
 (Ⅰ)设
(Ⅰ)设 是
是 上的一点,证明:平面
上的一点,证明:平面 平面
平面 ;
;
(Ⅱ)求四棱锥 的体积.
的体积.
 中,平面
中,平面 平面
平面 ,
, ,
, 是等边三角形,已知
是等边三角形,已知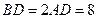 ,
, .
. (Ⅰ)设
(Ⅰ)设 是
是 上的一点,证明:平面
上的一点,证明:平面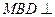 平面
平面 ;
;(Ⅱ)求四棱锥
 的体积.
的体积.(Ⅰ)证明略。
(Ⅱ) 。
。
(Ⅱ)
 。
。(Ⅰ)证明:在 中,由于
中,由于 ,
, ,
, ,所以
,所以 .故
.故 .又平面
.又平面 平面
平面 ,平面
,平面 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 ,又
,又 平面
平面 ,
,
 故平面
故平面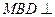 平面
平面 .
.
(Ⅱ)解:过 作
作 交
交 于
于 ,
,
由于平面 平面
平面 ,
,
所以 平面
平面 .因此
.因此 为四棱锥
为四棱锥 的高,
的高,
又 是边长为4的等边三角形.因此
是边长为4的等边三角形.因此 .
.
在底面四边形 中,
中, ,
, ,
,
所以四边形 是梯形,在
是梯形,在 中,斜边
中,斜边 边上的高为
边上的高为 ,
,
此即为梯形 的高,所以四边形
的高,所以四边形 的面积为
的面积为 .
.
故 .
.
 中,由于
中,由于 ,
, ,
, ,所以
,所以 .故
.故 .又平面
.又平面 平面
平面 ,平面
,平面 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 ,又
,又 平面
平面 ,
, 故平面
故平面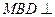 平面
平面 .
.(Ⅱ)解:过
 作
作 交
交 于
于 ,
,由于平面
 平面
平面 ,
,所以
 平面
平面 .因此
.因此 为四棱锥
为四棱锥 的高,
的高,又
 是边长为4的等边三角形.因此
是边长为4的等边三角形.因此 .
.在底面四边形
 中,
中, ,
, ,
,所以四边形
 是梯形,在
是梯形,在 中,斜边
中,斜边 边上的高为
边上的高为 ,
,此即为梯形
 的高,所以四边形
的高,所以四边形 的面积为
的面积为 .
.故
 .
.
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
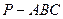 中,
中,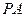 ^底面
^底面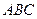 ,若底面
,若底面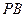 与底面
与底面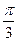 .若
.若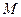 是
是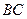 的中点,则三棱锥
的中点,则三棱锥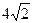

 π
π π
π π
π

 ,若使绕直线
,若使绕直线 旋转一周,则所形成的几何体的体积是( )
旋转一周,则所形成的几何体的体积是( )


