题目内容
2.向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,3),且$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$共线,则k=-1.分析 根据向量的坐标运算和向量共线的充要条件即可求出.
解答 解:∵$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,3),
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(0,5),k$\overrightarrow{a}$-$\overrightarrow{b}$=(k+1,2k-3),
∵$\overrightarrow{a}$+$\overrightarrow{b}$与k$\overrightarrow{a}$-$\overrightarrow{b}$共线,
∴5(k+1)=0,解得k=-1,
故答案为:-1.
点评 本题考查向量共线的充要条件,属基础题,熟记向量共线的充要条件是解决问题的基础.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
10.对整数n≥3,记f(n)=log23•log34…logn-1n,则f(22)+f(23)+…+f(210)=( )
| A. | 55 | B. | 1024 | C. | 54 | D. | 1000 |
14.若${(x+\frac{a}{{\root{3}{x}}})^8}$(a>0)的展开式中当且仅当第6项系数最大,则实数a的取值范围是( )
| A. | $\frac{5}{4}<a<2$ | B. | $\frac{5}{4}≤a≤2$ | C. | $2≤a≤\frac{7}{2}$ | D. | $2<a<\frac{7}{2}$ |
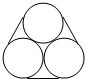 李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.
李师傅在建材商店购买了三根外围直径都为10cm的钢管,为了便于携带,他将三根钢管用铁丝紧紧捆住,截面如图所示,则铁丝捆扎一圈的长度为30+10πcm.