题目内容
12.在直角坐标系xOy中,直线y=x与抛物线x2=4y相交于O、A两点,则点A到抛物线焦点的距离为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 求出A的坐标,直接利用抛物线的定义,求解即可.
解答 解:因为直线y=x与抛物线x2=4y相交于O、A两点,
∴A(4,4)
点A到抛物线焦点的距离,就是这点到抛物线的准线的距离.
抛物线的准线方程为:y=-1,
所以点A到抛物线焦点的距离为4+1=5.
故选:A.
点评 本题考查抛物线的简单性质的应用,抛物线的定义的应用,考查计算能力.

练习册系列答案
相关题目
3.已知等比数列{an},{bn}的公比分别为q1,q2,则q1=q2是{an+bn}为等比数列的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.抛物线${C_1}:y=\frac{1}{2p}{x^2}(p>0)$的焦点与双曲线${C_2}:\frac{x^2}{8}-{y^2}=1$的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( )
| A. | $\frac{{7\sqrt{2}}}{16}$ | B. | $\frac{{7\sqrt{2}}}{8}$ | C. | $\frac{{21\sqrt{2}}}{8}$ | D. | $\frac{{21\sqrt{2}}}{4}$ |
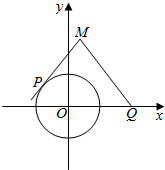 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.