题目内容
设f(x)=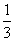 x3+mx2+nx,
x3+mx2+nx,
(1)如果g(x)=f′(x)-2x-3在x=-2处取得最小值-5,求f(x)的解析式;
(2)如果m+n<10(m,n∈N+),f(x)的单调递减区间的长度是正整数,试求m和n的值.(注:区间(a,b)的长度为b-a)
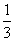 x3+mx2+nx,
x3+mx2+nx,(1)如果g(x)=f′(x)-2x-3在x=-2处取得最小值-5,求f(x)的解析式;
(2)如果m+n<10(m,n∈N+),f(x)的单调递减区间的长度是正整数,试求m和n的值.(注:区间(a,b)的长度为b-a)
解:(1)已知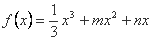 ,∴
,∴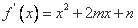 ,
,
又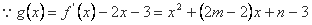 在x=-2处取极值,
在x=-2处取极值,
则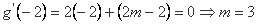 ,
,
又在x=-2处取最小值-5,
则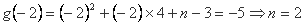 ,
,
∴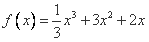 。
。
(2)要使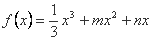 单调递减,则
单调递减,则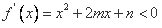 ,
,
又递减区间长度是正整数,所以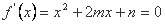 两根设做a,b,即有:b-a为区间长度。
两根设做a,b,即有:b-a为区间长度。
又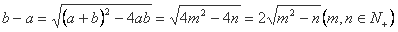 ,
,
又b-a为正整数,且m+n<10,
所以m=2,n=3或m=3,n=5符合。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目