题目内容
15.设函数f(x)在[1,+∞)上为增函数,f(3)=0,且g(x)=f(x+1)为偶函数,则不等式g(2-2x)<0的解集为(0,2).分析 根据函数的平移关系得到函数g(x)的单调递增区间,根据函数的单调性解不等式即可得到结论.
解答 解:∵f(x)在[1,+∞)上为增函数,
∴f(x)向左平移1个单位得到f(x+1),则f(x+1)在[0,+∞)上为增函数,
即g(x)在[0,+∞)上为增函数,
且g(2)=f(2+1)=0,
∵g(x)=f(x+1)为偶函数
∴不等式g(2-2x)<0等价为g(2-2x)<g(2),
即g(|2-2x|)<g(2),
则|2-2x|<2,
则-2<2x-2<2,
即0<2x<4,
则0<x<2,
即不等式的解集为(0,2),
故答案为:(0,2).
点评 本题主要考查函数单调性的应用,根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
3.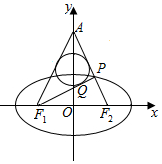 如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的左、右焦点分别为F1、F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则该椭圆的离心率为( )
如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的左、右焦点分别为F1、F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则该椭圆的离心率为( )
 如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的左、右焦点分别为F1、F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则该椭圆的离心率为( )
如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的左、右焦点分别为F1、F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则该椭圆的离心率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{\sqrt{13}}{4}$ |
10.设x,y满足约束条件$\left\{\begin{array}{l}{x≤3}\\{x+y≥0}\\{x-y+6≥0}\end{array}\right.$,若z=ax+y的最大值为3a+9,最小值为3a-3,则a的取值范围是( )
| A. | a≤-1 | B. | a≥1 | C. | -1≤a≤1 | D. | a≥1或a≤-1 |
20.某商业大厦有东南西3个大门,楼内东西两侧各有2个楼梯,从楼外到二楼的不同走法种数是( )
| A. | 5 | B. | 7 | C. | 10 | D. | 12 |