题目内容
已知椭圆x2+by2=3a与直线x+y-1=0相交于A、B两点（1）当
时，求实数b的取值范围；（2）当
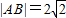时，AB的中点M与椭圆中心连线的斜率为
时，求椭圆的方程．
【答案】分析：（1）因为圆x2+by2=3a与直线x+y-1=0相交于A、B两点，所以方程组
有两相异实根，可以通过判别式△来判断．
（2）设A（x1，y1） B（x2，y2），由
，
，再根据中点坐标公式，和斜率公式可得．
解答：解：（1）解
∴x2（1+b）-2bx+b-3a=0
由题意得：△=4b2-4（1+b）（b-3a）＞0
解得b＜3
又因为b＞0且b≠1
∴0＜b＜3且b≠1
（2）设A（x1，y1） B（x2，y2） 由（1）
∴
整理得：b2+3b-3a-3ab+1=0，
AB中点M
由题意得：
∴b=5
∴a=
所求椭圆方程为
点评：本题考查了直线与椭圆位置关系的判断，做题时认真分析，找到切入点．
有两相异实根，可以通过判别式△来判断．（2）设A（x1，y1） B（x2，y2），由
，，再根据中点坐标公式，和斜率公式可得．解答：解：（1）解
∴x2（1+b）-2bx+b-3a=0
由题意得：△=4b2-4（1+b）（b-3a）＞0
解得b＜3
又因为b＞0且b≠1
∴0＜b＜3且b≠1
（2）设A（x1，y1） B（x2，y2） 由（1）
∴
整理得：b2+3b-3a-3ab+1=0，
AB中点M
由题意得：
∴b=5∴a=
所求椭圆方程为
点评：本题考查了直线与椭圆位置关系的判断，做题时认真分析，找到切入点．
练习册系列答案
相关题目