题目内容
已知正项数列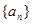 的前n项和
的前n项和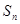 满足:
满足: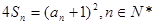 ,
,
(1)求数列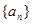 的通项
的通项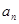 和前n项和
和前n项和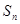 ;
;
(2)求数列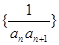 的前n项和
的前n项和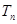 ;
;
(3)证明:不等式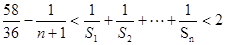 对任意的
对任意的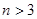 ,
,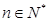 都成立.
都成立.
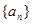 的前n项和
的前n项和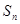 满足:
满足: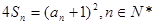 ,
,(1)求数列
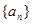 的通项
的通项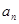 和前n项和
和前n项和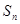 ;
;(2)求数列
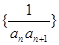 的前n项和
的前n项和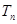 ;
;(3)证明:不等式
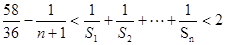 对任意的
对任意的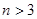 ,
,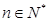 都成立.
都成立.(1)∴
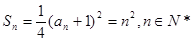
(2)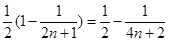 (3)见解析
(3)见解析

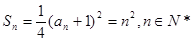
(2)
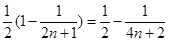 (3)见解析
(3)见解析第一问中,由于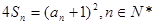 所以
所以
两式作差 ,然后得到
,然后得到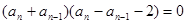
从而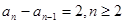 得到结论
得到结论
第二问中, 利用裂项求和的思想得到结论。
利用裂项求和的思想得到结论。
第三问中,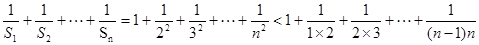
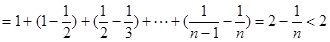
又

结合放缩法得到。
解:(1)∵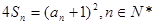 ∴
∴
∴
∴ ∴
∴ 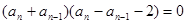 ………2分
………2分
又∵正项数列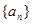 ,∴
,∴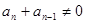 ∴
∴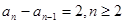
又n=1时,
∴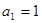 ∴数列
∴数列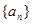 是以1为首项,2为公差的等差数列……………3分
是以1为首项,2为公差的等差数列……………3分
∴ …………………4分
…………………4分
∴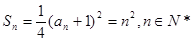 …………………5分
…………………5分
(2) …………………6分
…………………6分
∴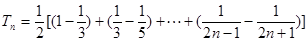
 …………………9分
…………………9分
(3)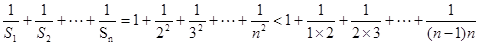
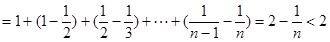 …………………12分
…………………12分
又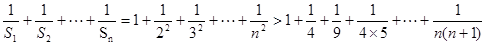

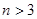 ,
,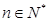
∴不等式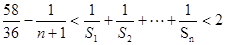 对任意的
对任意的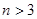 ,
,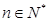 都成立.
都成立.
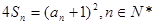 所以
所以
两式作差
 ,然后得到
,然后得到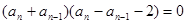
从而
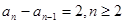 得到结论
得到结论第二问中,
 利用裂项求和的思想得到结论。
利用裂项求和的思想得到结论。第三问中,
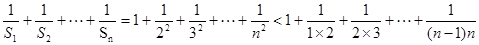
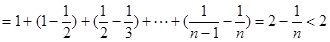
又


结合放缩法得到。
解:(1)∵
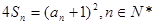 ∴
∴
∴

∴
 ∴
∴ 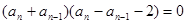 ………2分
………2分又∵正项数列
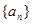 ,∴
,∴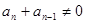 ∴
∴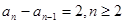
又n=1时,

∴
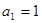 ∴数列
∴数列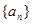 是以1为首项,2为公差的等差数列……………3分
是以1为首项,2为公差的等差数列……………3分∴
 …………………4分
…………………4分∴
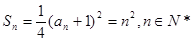 …………………5分
…………………5分 (2)
 …………………6分
…………………6分∴
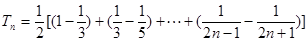
 …………………9分
…………………9分(3)
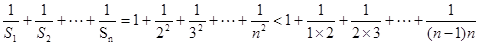
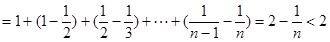 …………………12分
…………………12分又
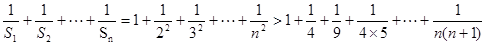

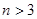 ,
,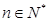
∴不等式
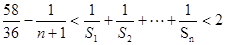 对任意的
对任意的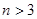 ,
,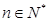 都成立.
都成立.
练习册系列答案
相关题目
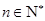 ,三个数A(n),B(n),C(n)组成公比为q的等比数列.
,三个数A(n),B(n),C(n)组成公比为q的等比数列.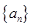 中,
中,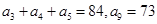 .
.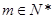 ,将数列
,将数列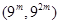 内的项的个数记为
内的项的个数记为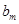 ,求数列
,求数列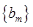 的前
的前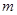 项和
项和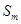 .
.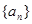 、
、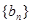 的前
的前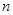 项和分别为
项和分别为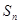 和
和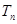 ,若
,若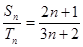 ,则
,则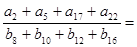 ( )
( )
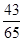
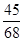
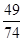
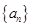 为等差数列,则下列数列中: (1)
为等差数列,则下列数列中: (1)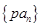 (2)
(2) 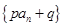 (3)
(3) 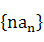 (4)
(4)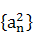 (5)
(5) 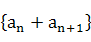 (其中p,q为常数)等差数列有 ________
(其中p,q为常数)等差数列有 ________  ,
, 的前
的前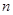 项和分别为
项和分别为 ,
,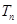 ,若
,若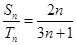 ,则
,则
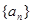 的前n项和
的前n项和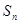 ,若
,若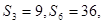 则
则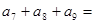 ( )
( )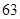
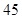

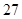
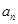 }是等差数列,平面内三点A、B、C共线,且
}是等差数列,平面内三点A、B、C共线,且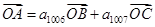 则数列{
则数列{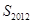 = ;
= ;