题目内容
在 中,角
中,角 所对的边分别为
所对的边分别为 ,设
,设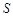 为
为 的面积,满足
的面积,满足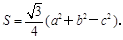
(Ⅰ)求角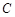 的大小;
的大小;
(Ⅱ)求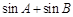 的最大值.
的最大值.
(Ⅰ)C=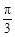 ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)将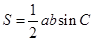 和
和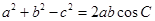 代入
代入 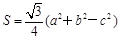 即可得tanC=
即可得tanC= ,故C=
,故C=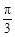 ;(Ⅱ)
;(Ⅱ)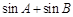 =sinA+sin(
=sinA+sin(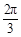 -A)=sinA+
-A)=sinA+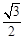 cosA+
cosA+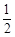 sinA=
sinA= sin(A+
sin(A+ ),再根据A的范围求得最大值为
),再根据A的范围求得最大值为 .
.
试题解析:(Ⅰ)由题意可知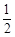 absinC=
absinC=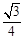 ·2abcosC,
·2abcosC,
所以tanC= .
.
因为0<C<π,所以C=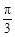 .
.
(Ⅱ)由已知sinA+sinB=sinA+sin(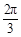 -A)=sinA+
-A)=sinA+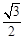 cosA+
cosA+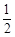 sinA
sinA
= sin(A+
sin(A+ ).
).
∵0<A<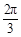 ,∴
,∴ <A+
<A+ <
< ,∴当A+
,∴当A+ =
=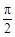 即A=
即A=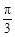 时,
时,
sinA+sinB的最大值是 .
.
考点:1.正弦定理;2.余弦定理;3.三角恒等变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的顶点
的顶点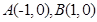 ,顶点
,顶点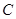 在直线
在直线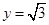 上;
上;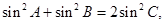 求点
求点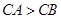 ,且
,且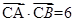 ,求角
,求角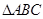 中,角
中,角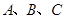 的对边分别为
的对边分别为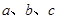 ,且有
,且有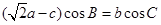 .
.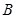 的大小;
的大小;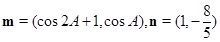 ,且
,且 ,求
,求 的值.
的值.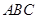 中,内角
中,内角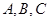 所对的边分别为
所对的边分别为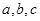 ,已知m
,已知m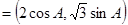 ,n
,n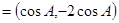 ,m·n
,m·n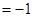 .
. 的大小;
的大小;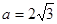 ,
, ,求△
,求△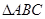 中,角
中,角 的对边分别为
的对边分别为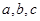 ,
, ,
,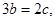
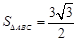 .
.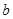 的值;
的值;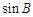 的值.
的值. 中,设
中,设 、
、 、
、 分别为角
分别为角 、
、 、
、 的对边,角
的对边,角 交
交 边于
边于 ,
,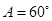 .
. ;
; ,
, ,求其三边
,求其三边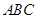 的三边为
的三边为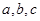 满足
满足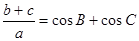 .
.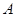 的值;
的值; 的取值范围.
的取值范围.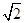 ,c=
,c= +1,求A
+1,求A