题目内容
(本题满分13分)
已知线段![]() ,
,![]() 的中点为
的中点为![]() ,动点
,动点![]() 满足
满足![]() (
(![]() 为正常数).
为正常数).
(Ⅰ)求动点![]() 所在的曲线方程;
所在的曲线方程;
(Ⅱ)若存在点![]() ,使
,使![]() ,试求
,试求![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,动点
,动点![]() 满足
满足![]() ,且
,且![]() ,试求
,试求![]() 面积的最大值和最小值.
面积的最大值和最小值.
解:(Ⅰ)以![]() 为圆心,
为圆心,![]() 所在直线为轴建立平面直角坐标系
所在直线为轴建立平面直角坐标系
若![]() ,即
,即![]() ,动点
,动点![]() 所在的曲线不存在;
所在的曲线不存在;
若![]() ,即
,即![]() ,动点
,动点![]() 所在的曲线方程为
所在的曲线方程为![]() ;
;
若![]() ,即
,即![]() ,动点
,动点![]() 所在的曲线方程为
所在的曲线方程为![]() .
.
………… 4分
(Ⅱ)由(Ⅰ)知![]() ,要存在点
,要存在点![]() ,使
,使![]() , 则以
, 则以![]() 为圆心,
为圆心,![]() 为半径的圆与椭圆有公共点。故
为半径的圆与椭圆有公共点。故![]() ,所以
,所以![]()
所以![]() 的取值范围是
的取值范围是![]() . …………8分
. …………8分
(Ⅲ)当![]() 时,其曲线方程为椭圆
时,其曲线方程为椭圆![]()
由条件知![]() 两点均在椭圆
两点均在椭圆![]() 上,且
上,且![]()
设![]() ,
,![]() ,
,![]() 的斜率为
的斜率为![]()
![]() ,则
,则![]() 的方程为
的方程为![]() ,
,
![]() 的方程为
的方程为![]()
解方程组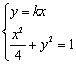 得
得![]() ,
,![]()
同理可求得![]() ,
,![]() …………10分
…………10分
![]() 面积
面积![]() =
=![]() …………11分
…………11分
令![]() 则
则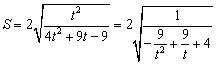
令![]()
所以![]() ,即
,即![]() …………13分
…………13分

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.