题目内容
10.f(x)是定义在D上的函数,若存在区间[m,n]⊆D,使函数f(x)在[m,n]上的值域恰为[km,kn],则称区间[m,n]为函数f(x)的k倍区间.若区间[m,n]为函数f(x)=$\frac{({a}^{2}+a)x-2}{{a}^{2}x}$(a≠0)的2倍区间,则n-m的最大值为$\frac{2\sqrt{15}}{15}$.分析 根据题目中的新定义,结合函数与方程的知识转化为$\frac{({a}^{2}+a)x-2}{{a}^{2}x}$=2的根求解,从而确定正确的答案.
解答 解:根据题意得出函数f(x)=$\frac{({a}^{2}+a)x-2}{{a}^{2}x}$(a≠0)=$\frac{{a}^{2}+a}{{a}^{2}}$$-\frac{2}{{a}^{2}x}$是单调递增函数,
∴转化为$\frac{({a}^{2}+a)x-2}{{a}^{2}x}$=2x有2个根的问题.
即2a2x2-(a2+a)x+2=0,
x1+x2=$\frac{{a}^{2}+a}{2{a}^{2}}$,xxx2=$\frac{1}{{a}^{2}}$,
|x1-x2|=$\sqrt{(\frac{{a}^{2}+a}{2{a}^{2}})^{2}-\frac{4}{{a}^{2}}}$═$\sqrt{\frac{{a}^{2}+2a-15}{4{a}^{2}}}$=$\sqrt{-\frac{15}{4}(\frac{1}{a})^{2}+\frac{1}{2}×\frac{1}{a}+\frac{1}{4}}$
根据二次函数得出$\frac{1}{a}$=$\frac{1}{15}$时取的最大值$\frac{2\sqrt{15}}{15}$
∵利用新定义判断n,m为方程的根
∴n-m的最大值为$\frac{2\sqrt{15}}{15}$
故答案为:$\frac{2\sqrt{15}}{15}$
点评 本题主要考查与函数有关的命题的真假判断,考查了在新定义下函数的定义域、值域问题以及解方程的问题,是易错题.综合性较强,有一定的难度.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,AB=2CB=2,∠ABC=60°,在梯形ACEF中,EF∥AC,且AC=2EF=2EC,EC⊥平面ABCD.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,AB=2CB=2,∠ABC=60°,在梯形ACEF中,EF∥AC,且AC=2EF=2EC,EC⊥平面ABCD.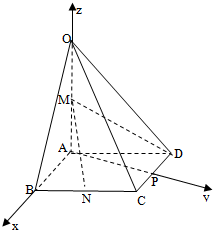 如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.
如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.