题目内容
选修4—5:不等式选讲
已知正实数 满足:
满足: .
.
(Ⅰ)求 的最小值
的最小值 ;
;
(II)设函数 ,对于(Ⅰ)中求得的
,对于(Ⅰ)中求得的 ,是否存在实数
,是否存在实数 使
使 成立,说明理由.
成立,说明理由.
(Ⅰ) ;(II)满足条件的实数
;(II)满足条件的实数 不存在.
不存在.
【解析】
试题分析:(Ⅰ)利用均值不等式,求得 的最小值;(II)利用含绝对值不等式的性质
的最小值;(II)利用含绝对值不等式的性质 (当且仅当
(当且仅当 同号时取“等号”)求得:
同号时取“等号”)求得:
 ,所以不存在符合条件的实数
,所以不存在符合条件的实数 .
.
试题解析:(Ⅰ)∵ 2ab 即  ∴
∴  2分
2分
(当 且仅当
且仅当 取等号).
取等号).
∴ ………5分
………5分
(II)
 9分
9分
∴ 满足条件的实数 不存在. 10分
不存在. 10分
考点:1.均值不等式;2.含绝对值不等式的性质.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
某小区在一次对 岁以上居民节能意识的问卷调查中,随机抽取了
岁以上居民节能意识的问卷调查中,随机抽取了 份问卷进行统计,得到相关的数据如下表:
份问卷进行统计,得到相关的数据如下表:
节能意识弱 | 节能意识强 | 总计 | |
| 45 | 9 | 54 |
大于50岁 | 10 | 36 | 46 |
总计 | 55 | 45 | 100 |
(Ⅰ)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(Ⅱ)若全小区节能意识强的人共有 人,则估计这
人,则估计这 人中,年龄大于
人中,年龄大于 岁的有多少人?
岁的有多少人?
(Ⅲ)按年龄分层抽样,从节能意识强的居民中抽 人,再从这
人,再从这 人中任取
人中任取 人,求恰
人,求恰
有1人年龄在 至
至 岁的概率。
岁的概率。
 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 B.
B. 
 D.
D. 
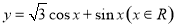 的图像向左平移个
的图像向左平移个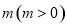 单位长度后,所得的图像关于
单位长度后,所得的图像关于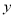 轴对称,则
轴对称,则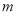 的最小值是
的最小值是  的首项
的首项 ,前
,前 项和为
项和为 ,且满足
,且满足 ,则满足
,则满足 的
的 的最大值为
的最大值为 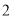 本不同的数学书和
本不同的数学书和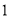 本语文书在书架上随机排成一行,则
本语文书在书架上随机排成一行,则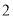 本数学书相邻的概率为
本数学书相邻的概率为 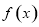 的定义域为
的定义域为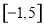 ,部分对应值如下表,
,部分对应值如下表,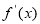 的图象如图所示.
的图象如图所示.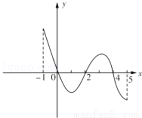
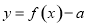 有
有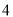 个零点,则实数
个零点,则实数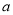 的取值范围为( )
的取值范围为( )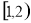 (B)
(B)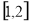 (C)
(C) 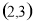 (D)
(D)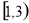
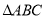 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为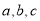 ,且
,且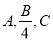 成等差数列.
成等差数列.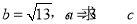 的值;
的值;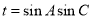 ,求t的最大值.
,求t的最大值. .
. =1时,函数
=1时,函数 取最小值,求实数
取最小值,求实数 的值;
的值; 的取值范围;
的取值范围; ,证明对任意正整数
,证明对任意正整数 ,不等式
,不等式 都成立.
都成立.