题目内容
8.已知正四面体A-BCD的棱长为2,点E是AD的中点,则下面四个命题中正确的是( )| A. | ?F∈BC,EF⊥AD | B. | ?F∈BC,EF⊥AC | C. | ?F∈BC,EF≥$\sqrt{3}$ | D. | ?F∈BC,EF∥AC |
分析 由题意画出图形,利用线面垂直的判定判定AD⊥面BCE,由此说明A正确;由三垂线定理结合∠BEC为锐角三角形说明B错误;举例说明C错误;由平面的斜线与平面内直线的位置关系说明D错误.
解答 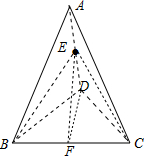 解:如图,
解:如图,
∵四面体A-BCD为正四面体,且E为AD的中点,
∴BE⊥AD,CE⊥AD,
又BE∩CE=E,∴AD⊥面BCE,则?F∈BC,EF⊥AD,选项A正确;
由AE⊥面BCE,∴AE⊥EF,若AC⊥EF,则CE⊥EF,
∵∠BEC为锐角三角形,∴不存在F∈BC,使EF⊥AC,选项B错误;
取BC中点F,可求得DF=$\sqrt{3}$,又DE=1,得EF=$\sqrt{2}$,选项C错误;
AC是平面BCE的一条斜线,∴AC与平面BCE内直线的位置关系是相交或异面,选项D错误.
故选:A.
点评 本题考查了命题的真假判断与应用,考查了空间中直线与平面的位置关系,考查了线线垂直与线面平行的判定,考查了空间想象能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.对归纳推理的表述不正确的一项是( )
| A. | 归纳推理是由部分到整体的推理 | |
| B. | 归纳推理是由个别到一般的推理 | |
| C. | 归纳推理是从研究对象的全体中抽取部分进行观察实验,以取得信息,从而对整体做出判断的一种推理 | |
| D. | 归纳推理是由一般到特殊的推理 |
 为奇函数,则
为奇函数,则 ______.
______. 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和. 不小于6”的概率;
不小于6”的概率; 为奇数”的概率和“
为奇数”的概率和“ 为偶数”的概率是不是相等?证明你作出的结论.
为偶数”的概率是不是相等?证明你作出的结论. ,若向量
,若向量 与向量
与向量 共线,则
共线,则 .
.