题目内容
13.设函数f(x)=$\left\{\begin{array}{l}{1,(sin\frac{π}{6}x≤\frac{1}{2})}\\{sin\frac{π}{6}x,(sin\frac{π}{6}x>\frac{1}{2})}\end{array}\right.$,g(x)=|x|+|6-x|,令F(x)=f(x)+g(x),若关于a的方程F(a2+a-1)=F(2a-m)有且仅有四个不等实根,则m的取值范围是(-$\frac{37}{4},-4-\sqrt{17})$$∪(-4-\sqrt{17},\sqrt{17}-4)∪(\sqrt{17}-4$,$\frac{5}{4})$..分析 根据f(x)的解析式结合正弦函数的周期性,得出f(x)的图象关于x=3对称,从而得出F((x)的对称性,作出函数的图象即可得m的取值范围.
解答  解:sin$[\frac{π}{6}(6-x)]$=sin($π-\frac{π}{6}x)$=sin$\frac{π}{6}x$
解:sin$[\frac{π}{6}(6-x)]$=sin($π-\frac{π}{6}x)$=sin$\frac{π}{6}x$
∴f(6-x)=f(x),
f(x)的图象关于x=3对称,
g(6-x)=g(x),
∴g(x)的图象关于x=3对称,
∴F(x)=f(x)+g(x)的图象关于x=3对称,即F(6-x)=F(x),
F(a2+a-1)=F(2a-m),
∴a2+a-1=2a-m或a2+a-1=6-(2a-m)
∴m=-a2+a+1或m=a2+3a-7,
要使方程有四个不等是跟,m的取值需要在C点以下,F点以上,且不包括:A(-$\frac{1+\sqrt{17}}{2},-4-\sqrt{17})$,B($\frac{-1+\sqrt{17}}{2},\sqrt{17}-4)$处的函数值,
故m的取值范围是(-$\frac{37}{4},-4-\sqrt{17})$$∪(-4-\sqrt{17},\sqrt{17}-4)∪(\sqrt{17}-4$,$\frac{5}{4})$.
点评 本题主要考查函数的图象和性质,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
8.已知正四面体A-BCD的棱长为2,点E是AD的中点,则下面四个命题中正确的是( )
| A. | ?F∈BC,EF⊥AD | B. | ?F∈BC,EF⊥AC | C. | ?F∈BC,EF≥$\sqrt{3}$ | D. | ?F∈BC,EF∥AC |
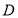 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数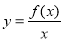 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间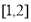 上不是“弱增”函数的为( )
上不是“弱增”函数的为( ) B.
B. C.
C. D.
D.