题目内容
如图,将两块三角板拼接成直二面角A-CB-D,其中DB⊥CB,∠DCB=30°,AB=AC,AB⊥AC,E、F分别是AB、BC的中点.(1)求证:EF∥平面ACD;
(2)求证:平面DEF⊥平面ABD.

【答案】分析:(1)由已知中,E、F分别是AB、BC的中点,根据三角形中位线定理,我们易得到EF∥AC,结合线面平行的判定定理,我们即可得到EF∥平面ACD;
(2)由已知中两块三角板拼接成直二面角A-CB-D,其中DB⊥CB,∠DCB=30°,AB=AC,AB⊥AC,我们易证明DB⊥AC,由(1)中的结论,我们进一步可以得到EF⊥平面ABD,结合面面垂直的判定定理,即可得到平面DEF⊥平面ABD.
解答:证明:(1)∵E,F分别为AB,CB中点,∴EF∥AC,(3分)
∵EF不在平面ACD中,AC在平面ACD中,∴EF∥ACD中(6分)
(2)∵平面DBC⊥平面ABC,平面DBC\cap平面ABC=BC,DB⊥BC,DB在平面BCD中∴DB⊥平面ABC,(8分)
又AC在平面ABC中∴DB⊥AC,∵EF∥AC,(11分)
∴EF⊥BD,EF⊥AB,∵AB∩BD=B,∴EF⊥平面ABD,
又EF在平面DEF中,∴平面DEF⊥平面ABD.(14分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,熟练掌握空间直线与平面位置关系的判定定理及证明步骤是解答此类问题的关键.
(2)由已知中两块三角板拼接成直二面角A-CB-D,其中DB⊥CB,∠DCB=30°,AB=AC,AB⊥AC,我们易证明DB⊥AC,由(1)中的结论,我们进一步可以得到EF⊥平面ABD,结合面面垂直的判定定理,即可得到平面DEF⊥平面ABD.
解答:证明:(1)∵E,F分别为AB,CB中点,∴EF∥AC,(3分)
∵EF不在平面ACD中,AC在平面ACD中,∴EF∥ACD中(6分)
(2)∵平面DBC⊥平面ABC,平面DBC\cap平面ABC=BC,DB⊥BC,DB在平面BCD中∴DB⊥平面ABC,(8分)
又AC在平面ABC中∴DB⊥AC,∵EF∥AC,(11分)
∴EF⊥BD,EF⊥AB,∵AB∩BD=B,∴EF⊥平面ABD,
又EF在平面DEF中,∴平面DEF⊥平面ABD.(14分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,熟练掌握空间直线与平面位置关系的判定定理及证明步骤是解答此类问题的关键.

练习册系列答案
相关题目
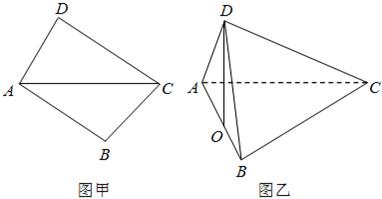 将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙. 如图,将两块直角三角板拼在一起,若
如图,将两块直角三角板拼在一起,若 (2008•襄阳模拟)将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
(2008•襄阳模拟)将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙. 如图,将两块直角三角板拼在一起,若
如图,将两块直角三角板拼在一起,若 ,
, ,则x=________.
,则x=________. ,
, ,则x= .
,则x= .