题目内容
如图，过圆E外一点A作一条直线与圆E交于B，C两点，且AB＝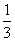
AC，作直线AF与圆E相切于点F，连接EF交BC于点D，已知圆E的半径为2，∠EBC＝30°.
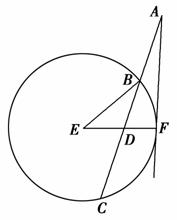
(1)求AF的长；
(2)求证：AD＝3ED.
(1)延长BE交圆E于点M，连接CM，则∠BCM＝90°，又BM＝2BE＝4，∠EBC＝30°，所以BC＝2
.
又AB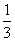＝AC，则AB＝
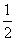BC＝，
所以根据切割线定理得，AF2＝AB·AC＝×3＝9，即AF＝3.
(2)过点E作EH⊥BC于点H，则EH＝
＝1，且△EDH与△ADF相似，
从而有
＝
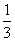＝，因此AD＝3ED.
练习册系列答案
相关题目
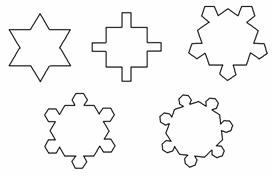
)到直线l：ρcos(θ＋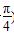
)＝
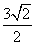上的点的最短距离为________．
＋
≥a＋b；
(0<x<1)的最小值．