题目内容

18．已知函数f（x）=ex-（x+1）2（e为自然对数的底数），则f（x）的大致图象是（　　）
A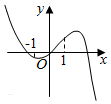．B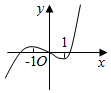．C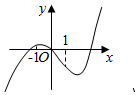．D．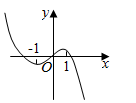

分析 求出导函数，利用导函数判断函数的单调性．根据数形结合，画出函数的图象，得出交点的横坐标的范围，根据范围判断函数的单调性得出选项．

解答 解：f'（x）=ex-2（x+1）=0，
相当于函数y=ex和函数y=2（x+1）交点的横坐标，画出函数图象如图
由图可知-1＜x1＜0，x2＞1，且x＞x2时，f'（x）＞0，递增，
故选C

点评 考查了导函数的应用和利用数形结合的方法判断极值点位置．

练习册系列答案
相关题目
8．关于函数f（x）=sin2x+sinx+cosx，以下说法：
①周期为2π；②最小值为-$\frac{5}{4}$；③在区间（0，$\frac{π}{2}$）单调递增；④关于x=$\frac{π}{4}$对称，
其中正确的是①②④（填上所有正确说法的序号）．
9．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{1}{2}$，且经过点$P（1，\frac{3}{2}）$，两个焦点分别为F1，F2．
（1）求椭圆C的方程；
（2）过F1的直线l与椭圆C相交于A，B两点，若△AF2B的内切圆半径为$\frac{{3\sqrt{2}}}{7}$，求以F2为圆心且与直线l相切的圆的方程．
6．已知α，β表示两个不同平面，a，b表示两条不同直线，对于下列两个命题：
①若b?α，a?α，则“a∥b”是“a∥α”的充分不必要条件
②若a?α，b?α，则“α∥β”是“α∥β且b∥β”的充要条件．
判断正确的是（　　）
A．①，②是真命题B．①是真命题，②是假命题
C．①是假命题，②是真命题D．①，②都是假命题
13．已知集合A={0，1，2}，则集合B={x-y|x∈A，y∈A}的元素个数为（　　）
A．4B．5C．6D．9
3．等腰直角△ABC中，∠A=$\frac{π}{2}$，AC=1，BC在x轴上，有-个半径为1的圆P沿x轴向△ABC滚动，并沿△ABC的表面滚过，则圆心P的大致轨迹是（虚线为各段弧所在圆的半径）（　　）
A．B．C．D．
10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A，上顶点为B，直线AB的斜率为$\frac{\sqrt{6}}{6}$，坐标原点O到直线AB的距离为$\frac{\sqrt{42}}{7}$．
（I）求椭圆C的标准方程；
（Ⅱ）是否在圆O：x2+y2=b2上存在点D，使得圆O过点D的切线与椭圆C交于点P，Q，线段PQ的中点为M，直线PQ与OM的夹角为45°？若存在，求点D的横坐标；若不存在，说明理由．
7．在平面直角坐标系中，已知三个点列{An}、{Bn}、{Cn}，其中An（n，an）、Bn（n，bn）、Cn（n-1，0），满足向量$\overrightarrow{{A}_{n}{A}_{n+1}}$与向量$\overrightarrow{{B}_{n}{C}_{n}}$共线，且bn+1-bn=6，a1=b1=0，则an=3n2-9n+6（n∈N*）．（用n表示）
8．在一宝宝“抓周”的仪式上，在宝宝面前摆着4件学习用品，3件生活用品，4件娱乐用品，若他只抓其中的一件物品，则他抓的结果有10．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网