��Ŀ����
6����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������㣨$\sqrt{3}$��$\frac{1}{2}$����������Ϊ$\frac{\sqrt{3}}{2}$�������Ҷ���ֱ�ΪA��B��ֱ��l1��x=-2��ֱ��l2��y=2����1������ԲC�ķ��̣�
��2�����P����ԲC����x���Ϸ���һ�����㣬ֱ��AP��ֱ��l2���ڵ�M��ֱ��BP��ֱ��l1���ڵ�N����ֱ��MN��б�ʵ�ȡֵ��Χ��
���� ��1������$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����a��b��c���ɵó���
��2����P��x0��y0������${x}_{0}^{2}+4{y}_{0}^{2}=4$���ɵ�kAP•kBP=-$\frac{1}{4}$����kAP=k���ɵ�kBP=-$\frac{1}{4k}$��ֱ��AP�ķ���Ϊ��y=k��x+2�����ɵ�M$��\frac{2-2k}{k}��2��$��ͬ���ɵã�N$��-2��\frac{1}{k}��$�����ɵó�kMN��
��� �⣺��1������$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����a=2��b=1��c=$\sqrt{3}$��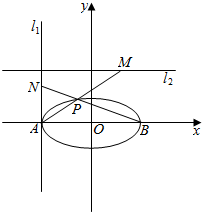
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2����P��x0��y0������${x}_{0}^{2}+4{y}_{0}^{2}=4$��
kAP•kBP=$\frac{{y}_{0}}{{x}_{0}+2}$•$\frac{{y}_{0}}{{x}_{0}-2}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-4}$=-$\frac{1}{4}$��
��kAP=k����kBP=-$\frac{1}{4k}$��
ֱ��AP�ķ���Ϊ��y=k��x+2������M$��\frac{2-2k}{k}��2��$��
ֱ��BP�ķ���Ϊ��y=$-\frac{1}{4k}$��x-2������N$��-2��\frac{1}{k}��$��
��kMN=$\frac{2-\frac{1}{k}}{\frac{2-2k}{k}+2}$=k-$\frac{1}{2}$��
��k��0��
��kMN=k-$\frac{1}{2}$$��-\frac{1}{2}$��
��ֱ��MN��б�ʵ�ȡֵ��Χ��$��-\frac{1}{2}��+�ޣ�$��
���� ���⿼������Բ�ı����̼������ʡ�б�ʼ��㹫ʽ�������ĵ����ԣ���������������������������������⣮

| A�� | 25�� | B�� | 15 �� | C�� | 30 �� | D�� | 20�� |
| A�� | [1��+�ޣ� | B�� | ��-�ޣ�2] | C�� | [2��3] | D�� | [1��3] |
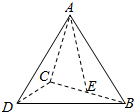 ����A-BCD�У�E��BC���е㣬AB=AD��BD��DC����֤��AE��BD��
����A-BCD�У�E��BC���е㣬AB=AD��BD��DC����֤��AE��BD��