题目内容
17.在△ABC中,A=120°,c>b,a=$\sqrt{21}$,S△ABC=$\sqrt{3}$,求:(1)边b,c的值.
(2)sinB+cosC的值.
分析 (1)利用三角形的面积公式与余弦定理,列出方程组即可求出b、c的值;
(2)由正弦定理和余弦定理分别求出sinB、cosC的值即可.
解答 解:(1)△ABC中,A=120°,
S△ABC=$\frac{1}{2}$bcsinA=$\sqrt{3}$,
∴bc=4,
又a2=b2+c2-2bccosA,
∴b2+c2-2bc×(-$\frac{1}{2}$)=21
∴b2+2bc+c2=25
∴b+c=5,
而c>b
所以b=1,c=4
(2)由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:
$\frac{\sqrt{21}}{sin120°}$=$\frac{1}{sinB}$,
所以sinB=$\frac{\sqrt{7}}{14}$;
由余弦定理cosC=$\frac{a2+b2-c2}{2ab}$得:
cosC=$\frac{\sqrt{21}}{7}$,
所以sinB+cosC=$\frac{\sqrt{7}+2\sqrt{21}}{14}$.
点评 本题考查了正弦、余弦定理的综合应用问题,是基础题目.

练习册系列答案
相关题目
2.在空间直角坐标系中,若A(2,-2,1),B(4,2,3),C(x,y,2)三点共线,则$\left|\overrightarrow{BC}\right|$=( )
| A. | $\sqrt{6}$ | B. | $2\sqrt{6}$ | C. | $\sqrt{5}$ | D. | $2\sqrt{5}$ |
9.由三条直线x=0、x=2、y=0和曲线y=x3所围成的图形的面积为( )
| A. | 8 | B. | $\frac{4}{3}$ | C. | $\frac{18}{5}$ | D. | 4 |
 在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.
在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.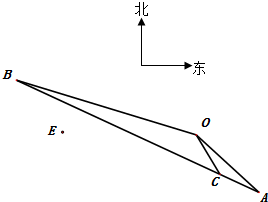 如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).
如图,某自行车手从O点出发,沿折线O-A-B-O匀速骑行,其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°-α)(其中sinα=$\frac{1}{{\sqrt{26}}}$,0°<α<90°)且与点O相距5$\sqrt{13}$千米(假设所有路面及观测点都在同一水平面上).