题目内容
下列四个图中,函数 的图象可能是( )
的图象可能是( )
C
解析试题分析:解:函数 的图象可以看作是由函数
的图象可以看作是由函数 的图象向左移动1个单位得到的,
的图象向左移动1个单位得到的,
而函数 是奇函数,所以排除
是奇函数,所以排除 和
和 ;
;
又因为当 时,
时,
所以选C。
考点:1、函数图象的变换;2、函数的奇偶性;3、对数函数的性质.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
下列函数,在其定义域内既是奇函数又是增函数的是 ( )
A.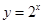  | B.  |
C.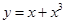  | D.  |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
已知 是
是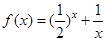 的一个零点,
的一个零点, ,则 ( )
,则 ( )
A. | B. |
C. | D. |
若 ,且
,且 .则下列结论正确的是( )
.则下列结论正确的是( )
A. | B. | C. | D. |
“ ”是“函数
”是“函数 在区间
在区间 内单调递增”的( )
内单调递增”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
函数y=f(x)在(0,2)上是增函数,函数y=f(x+2)是偶函数,则f(1),f(2.5),f(3.5)的大小关系是( )
| A.f(2.5)<f(1)<f(3.5) |
| B.f(2.5)>f(1)>f(3.5) |
| C.f(3.5)>f(2.5)>f(1) |
| D.f(1)>f(3.5)>f(2.5) |
设f(x)为定义在R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)等于( )
| A.-3 | B.-1 | C.1 | D.3 |
 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).

