若,且．则下列结论正确的是 A． B． C． D．题目和参考答案——青夏教育精英家教网—

题目内容

若,且．则下列结论正确的是( )

A．

B．

C．

D．

解析试题分析：考察函数，首先它是偶函数，其次在时，与都是增函数，且均不小于0，因此可证在上也是增函数.由得，即，∴，选D.
考点：函数的单调性与奇偶性.

练习册系列答案

课课练与单元测试系列答案

相关题目

实数x,y满足，若函数z=x+y的最大值为4,则实数a的值为( )

已知定义在上的函数满足为奇函数，函数关于直线对称，则下列式子一定成立的是（）

A．	B．
C．	D．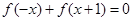

已知的定义域为，则函数的定义域为 ( )

下列四个图中，函数的图象可能是（）

已知圆及以下三个函数：①；②；③．其中图象能等分圆面积的函数个数为（）

若关于x的方程有五个互不相等的实根，则k的取值范围是

A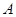．	B．
C．	D．

下列函数中，与函数的奇偶性、单调性均相同的是（）

已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=a^x-a^-x+2(a>0且a≠1),若g(2)=a,则f(2)等于(　　)

A．2	B．
C．	D．a²

试题分类