题目内容
已知直线x+y+2=0截圆x2+y2=z2所得弦的长度为4,则圆半径为( )
| A、2 | ||
B、
| ||
| C、6 | ||
D、
|
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:把圆的方程化为标准形式,求出弦心距,再由条件根据弦长公式求得z的值
解答:
解:由题意,弦心距d=
=
.
∵直线x+y+2=0截圆x2+y2=z2所得弦的长度为4,
∴由弦长公式可得2
=4,∴|z|=
;
故选:D.
| 2 | ||
|
| 2 |
∵直线x+y+2=0截圆x2+y2=z2所得弦的长度为4,
∴由弦长公式可得2
| z2-2 |
| 6 |
故选:D.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
有一个同学开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表,画出散点图后,求得热饮杯
关于当天气温x(°C)的回归方程为
=-2.352x+147.767.如果某天的气温是40°C则这天大约可以卖出的热饮杯数是( )
 |
| y |
 |
| y |
| A、51 | B、53 | C、55 | D、56 |
如图所示:执行如图所示的程序框,则输出的M的值为( )


| A、6 | B、7 | C、8 | D、9 |
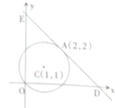 已知圆C的方程为(x-1)2+(y-1)2=2,点A(2,2).
已知圆C的方程为(x-1)2+(y-1)2=2,点A(2,2).