题目内容
14．若sinα=-$\frac{\sqrt{10}}{10}$，且α为第四象限角，则tanα的值等于（ ）| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |
分析 由sinα的值及α为第四象限角，利用同角三角函数间的基本关系求出cosα的值，即可确定出tanα的值．
解答 解：∵sinα=-$\frac{\sqrt{10}}{10}$，且α为第四象限角，
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{3\sqrt{10}}{10}$，
则tanα=-$\frac{1}{3}$，
故选：B．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
2．下列函数中，是偶函数且在区间（0，+∞）上是减函数的是（ ）
| A． | $f（x）=\frac{1}{x^2}$ | B． | f（x）=x2 | C． | $f（x）=\frac{1}{x}$ | D． | f（x）=lnx |
6．对任意$x∈（{0，\frac{π}{2}}）$，不等式sinx•f（x）＜cosx•f′（x）恒成立，则下列不等式错误的是（ ）
| A． | $f（{\frac{π}{3}}）＞\sqrt{2}f（{\frac{π}{4}}）$ | B． | $f（{\frac{π}{3}}）＞2cos1•f（1）$ | C． | $f（{\frac{π}{4}}）＜\sqrt{2}cos1•f（1）$ | D． | $f（{\frac{π}{4}}）＜\frac{{\sqrt{6}}}{2}f（{\frac{π}{6}}）$ |
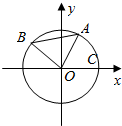已知A，B是单位圆O上的动点，且A，B分别在第一，二象限．C是圆与x轴正半轴的交点，△AOB为正三角形，记∠AOC=α