题目内容
4.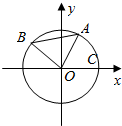 已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α
已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α(1)若A点的横坐标为$\frac{3}{5}$,求tan(540°-α)的值;
(2)若tan(α+60°)=-$\frac{3}{4}$,求B、C两点之间的距离.
分析 (1)可得A点纵坐标为$\frac{4}{5}$,由三角函数的定义可得tanα=$\frac{4}{3}$,由诱导公式可得;
(2)由题意可得tan∠COB=-$\frac{3}{4}$,进而可得B(-$\frac{4}{5}$,-$\frac{3}{5}$),由两点之间的距离公式可得.
解答 解:(1)当A点的横坐标为$\frac{3}{5}$时,纵坐标为$\frac{4}{5}$,
∴由三角函数的定义可得tanα=$\frac{4}{3}$,
∴tan(540°-α)=tan(180°×3-α)=-tanα=-$\frac{4}{3}$;
(2)∵tan(α+60°)=tan∠COB=-$\frac{3}{4}$,
∴B(-$\frac{4}{5}$,-$\frac{3}{5}$),又C(1,0),
∴B、C两点之间的距离为$\sqrt{(-\frac{4}{5}-1)^{2}+(-\frac{3}{5}-0)^{2}}$=$\frac{3\sqrt{10}}{25}$
点评 本题考查三角函数的定义,涉及两点间的距离公式,属基础题.

练习册系列答案
相关题目
14.若sinα=-$\frac{\sqrt{10}}{10}$,且α为第四象限角,则tanα的值等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
15.sin2(π+α)-cos(π+α)cosα+1的值是( )
| A. | 2 | B. | 1 | C. | 2sin2α | D. | 0 |
16.若曲线C1,y=x2与曲线C2:y=aex存在公切线,则a的( )
| A. | 最大值为$\frac{8}{{e}^{2}}$ | B. | 最大值为$\frac{4}{{e}^{2}}$ | C. | 最小值为$\frac{8}{{e}^{2}}$ | D. | 最小值为$\frac{4}{{e}^{2}}$ |
14.已知m∈R,函数f(x)=$\left\{\begin{array}{l}{|x+1|,}&{x<1}\\{lg(x-1),}&{x>1}\end{array}\right.$,g(x)=x2-2x+2m-2,若函数y=f(g(x))-m有6个零点,则实数m的取值范围是( )
| A. | (1,2) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{2}{3}$,$\frac{3}{4}$) | D. | (0,$\frac{2}{3}$) |