题目内容
19.已知椭圆C:$\frac{x^2}{3}+{y^2}$=1,斜率为1的直线l与椭圆C交于A,B两点,且|AB|=$\frac{{3\sqrt{2}}}{2}$,则直线l的方程为y=x±1.分析 设出直线方程y=x+m,代入x2+3y2=3,结合题设条件利用椭圆的弦长公式能求出m,得到直线方程.
解答 解:椭圆:$\frac{x^2}{3}+{y^2}$=1,即:x2+3y2=3
l:y=x+m,代入x2+3y2=3,
整理得4x2+6mx+3m2-3=0,
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{6m}{4}$,x1x2=$\frac{3{m}^{2}-3}{4}$,
|AB|=$\sqrt{1+{1}^{2}}$•|x1-x2|
=$\sqrt{2}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{2}×\sqrt{(-\frac{6m}{4})^{2}-4×\frac{3{m}^{2}-3}{4}}$=$\frac{{3\sqrt{2}}}{2}$,.
解得:m=±1.
直线l:y=x±1.
故答案为:y=x±1.
点评 本题考查椭圆弦长的求法,解题时要注意弦长公式,考查计算能力以及分析问题解决问题的能力.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
7.如果命题p(n)对n=k成立,则它对n=k+2也成立,若p(n)对n=2成立,则下列结论正确的是( )
| A. | p(n)对所有正整数n都成立 | B. | p(n)对所有正偶数n都成立 | ||
| C. | p(n)对大于或等于2的正整数n都成立 | D. | p(n)对所有自然数都成立 |
 某3D打印机,其打出的产品质量按照百分制衡量,若得分不低于85分则为合格品,低于85分则为不合格品,商家用该打印机随机打印了15件产品,得分情况如图;
某3D打印机,其打出的产品质量按照百分制衡量,若得分不低于85分则为合格品,低于85分则为不合格品,商家用该打印机随机打印了15件产品,得分情况如图; ,
, ,若
,若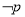 是
是 的充分而不必要条件,求实数
的充分而不必要条件,求实数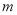 的取值范围.
的取值范围.