题目内容
14.已知F1,F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,A是其上顶点,且△AF1F2是等腰直角三角形,延长AF2与椭圆C交于另一点B,若△AF1B的面积是8,则椭圆C的方程是$\frac{x^2}{{{{12}^{\;}}}}+\frac{y^2}{6}=1$.分析 由△AF1F2是等腰直角三角形,可得b=c,可设椭圆的标准方程为:$\frac{{x}^{2}}{{2b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(b>0).在Rt△ABF1中,由勾股定理可得:丨AF1丨2+|AB|2=丨F2B丨2,|AF2|=|AF1|=$\sqrt{2}$b,设|BF2|=m,则|BF1|=2a-m=2$\sqrt{2}$b-m,2b2+($\sqrt{2}$b+m)2=(2$\sqrt{2}$b-m)2,又S=$\frac{1}{2}$丨AF1丨•丨AB丨=$\frac{1}{2}$×$\sqrt{2}$($\sqrt{2}$b+m)=8,联立解出即可得出b2,即可求得椭圆C的标准方程.
解答 解:∵△AF1F2是等腰直角三角形,b=c,
可设椭圆的标准方程为:$\frac{{x}^{2}}{{2b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(b>0).
在Rt△ABF1中,由勾股定理可得:丨AF1丨2+|AB|2=丨F2B丨2,
|AF2|=|AF1|=$\sqrt{2}$b,设|BF2|=m,则|BF1|=2a-m=2$\sqrt{2}$b-m,
代入可得:2b2+($\sqrt{2}$b+m)2=(2$\sqrt{2}$b-m)2,
又△AF1B的面积S=$\frac{1}{2}$丨AF1丨•丨AB丨=$\frac{1}{2}$×$\sqrt{2}$($\sqrt{2}$b+m)=8,
联立解得:b2=6,
∴椭圆的标准方程为:$\frac{x^2}{{{{12}^{\;}}}}+\frac{y^2}{6}=1$.
故答案为:$\frac{x^2}{{{{12}^{\;}}}}+\frac{y^2}{6}=1$.
点评 本题考查了椭圆的定义标准方程及其性质、勾股定理、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案| 性别 科目 | 男 | 女 |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
(2)用独立性检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?
| A. | 2$\sqrt{2}$-3 | B. | 2$\sqrt{2}$-1 | C. | 2$\sqrt{2}$+3 | D. | 2$\sqrt{2}$+1 |
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{11}{3}$ | D. | $\frac{1}{14}$ |
| 课程 | 数学1 | 数学2 | 数学3 | 数学4 | 数学5 | 合计 |
| 选课人数 | 180 | 540 | 540 | 360 | 180 | 1800 |
(1)从选出的10名学生中随机抽取3人,求这3人中至少有2人选择数学2的概率;
(2)从选出的10名学生中随机抽取3人,记这3人中选择数学2的人数为X,选择数学1的人数为Y,设随机变量ξ=X-Y,求随机变量ξ的分布列和数学期望E(ξ).
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,且AB=AC=2,O为AC的中点,PO⊥平面ABCD,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,且AB=AC=2,O为AC的中点,PO⊥平面ABCD,M为PD的中点. ,
, ,(
,(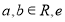 为自然对数的底数),且曲线
为自然对数的底数),且曲线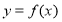 与
与 在坐标原点处的切线相同.
在坐标原点处的切线相同.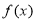 的最小值;
的最小值; 时,
时, 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.