题目内容
13.已知盒中装有3只螺口灯泡与7只卡口灯泡,这些灯泡的外形与功率都相同且灯口向下放着,现需要一只卡口灯泡,电工师傅每次从中任取一只并不放回,则在他第1次抽到的是螺口灯泡的条件下,第2次抽到的是卡口灯泡的概率是$\frac{7}{9}$.分析 把本题转化为古典概率来解,他第2次抽到时,盒子中还有2只螺口灯泡与7只卡口灯泡,根据古典概率计算公式求得他第2次抽到的是卡口灯泡的概率.
解答 解:在他第1次抽到的是螺口灯泡的条件下,这时盒子中还有2只螺口灯泡与7只卡口灯泡,
这时,第2次抽到的是卡口灯泡的概率为 $\frac{7}{7+2}$=$\frac{7}{9}$,
故答案为:$\frac{7}{9}$.
点评 本题主要考查古典概型及其概率计算公式的应用,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
4.设数列{an}的前n项和为Sn,若Sn=n2+2n(n∈N*),则$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=( )
| A. | $\frac{1}{3}-\frac{1}{2n+1}$ | B. | $\frac{1}{3}-\frac{1}{2n+3}$ | C. | $\frac{1}{6}-\frac{1}{4n+3}$ | D. | $\frac{1}{6}-\frac{1}{4n+6}$ |
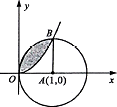 如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.
如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.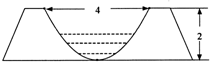 为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.
为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.