题目内容
8.在直角坐标系xoy中,直线l的方程为x-y+4=0.以原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2-4$\sqrt{2}$ρcos(θ-$\frac{π}{4}$)+6=0.(1)求直线l的极坐标方程,曲线C的直角坐标方程;
(2)若点P曲线C上任意一点,P点的直角坐标为(x,y),求x+2y的最大值和最小值.
分析 (1)把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得直线l的极坐标方程.把曲线C的极坐标方程展开可得:ρ2-4$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)+6=0,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$及其ρ2=x2+y2代入即可得出直角坐标方程.
(2)x2+y2-4x-4y+6=0,配方化为:(x-2)2+(y-2)2=2,圆心C(2,2),半径r=$\sqrt{2}$.设x+2y=t,则圆心C到直线的距离d=$\frac{|2+4-t|}{\sqrt{5}}$≤$\sqrt{2}$,解出即可得出.
解答 解:(1)直线l的方程为x-y+4=0.把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得直线l的极坐标方程:ρcosθ-ρsinθ+4=0.
曲线C的极坐标方程为ρ2-4$\sqrt{2}$ρcos(θ-$\frac{π}{4}$)+6=0,展开可得:ρ2-4$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)+6=0,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$及其ρ2=x2+y2代入可得:x2+y2-4x-4y+6=0.
(2)x2+y2-4x-4y+6=0,配方化为:(x-2)2+(y-2)2=2,圆心C(2,2),半径r=$\sqrt{2}$.
设x+2y=t,则圆心C到直线的距离d=$\frac{|2+4-t|}{\sqrt{5}}$≤$\sqrt{2}$,
解得$10-\sqrt{6}$≤t≤10+$\sqrt{6}$.
∴x+2y的最小值和最大值分别为:$10-\sqrt{6}$;10+$\sqrt{6}$.
点评 本题考查了极坐标方程与直角坐标方程的互化、直线与圆的位置关系、和差化积,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{a+b}{2}$ | B. | a+b | C. | $\frac{{a}^{2}-{b}^{2}}{2}$ | D. | $\frac{{b}^{2}-{a}^{2}}{2}$ |
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
| A. | (-1,2) | B. | (-2,1) | C. | [-2,2) | D. | [-2,+∞) |
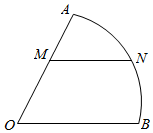 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.