题目内容
9.已知f(x)=$\sqrt{{x}^{2}-1}$,试判断f(x)在[1,+∞)上的单调性,并证明.分析 运用单调性的定义判断得出:f(x1)-f(x2)=$\sqrt{{{x}_{1}}^{2}-1}$$-\sqrt{{{x}_{2}}^{2}-1}$=$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{\sqrt{{{x}_{1}}^{2}-1}+\sqrt{{{x}_{2}}^{2}-1}}$,运用定义判断符号,就可以得出f(x1)<f(x2),利用单调性的定义判断即可.
解答 证明:设x1,x2∈[1,+∞),且x1<x2.
f(x1)-f(x2)=$\sqrt{{{x}_{1}}^{2}-1}$$-\sqrt{{{x}_{2}}^{2}-1}$=$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{\sqrt{{{x}_{1}}^{2}-1}+\sqrt{{{x}_{2}}^{2}-1}}$
∵x1,x2∈[1,+∞),且x1<x2.
∴x1-x2<0,x1+x2>0,$\sqrt{{{x}_{1}}^{2}-1}$≥0,$\sqrt{{{x}_{2}}^{2}-1}$>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在[1,+∞)上的单调递增.
点评 本题考查了函数的单调性的定义,关键是利用差比法分解因式,难度不大,属于中档题.

练习册系列答案
相关题目
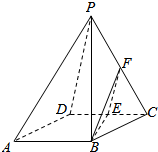 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.