题目内容
【题目】如图,在平面直角坐标系 ![]() 中,已知椭圆
中,已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,C为椭圆上位于第一象限内的一点.
,C为椭圆上位于第一象限内的一点.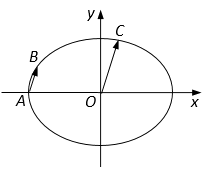
(1)若点 ![]() 的坐标为
的坐标为 ![]() ,求a,b的值;
,求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且 ![]() ,求直线AB的斜率.
,求直线AB的斜率.
【答案】
(1)
解:因为椭圆的离心率为 ![]() ,
,
所以 ![]() ,即
,即 ![]() .①
.①
又因为点 ![]()
![]() 在椭圆上,
在椭圆上,
所以 ![]() . ②
. ②
由①②解得 ![]() .
.
因为 ![]() ,所以
,所以 ![]() .
.
(2)
法一:由①知, ![]() ,所以椭圆方程为
,所以椭圆方程为 ![]() ,即
,即 ![]() .
.
设直线OC的方程为 ![]()
![]() ,
, ![]() ,
, ![]() .
.
由 ![]() 得
得 ![]() ,
,
所以 ![]() .因为
.因为 ![]() ,所以
,所以 ![]() .
.
因为 ![]() ,所以
,所以 ![]() .可设直线
.可设直线 ![]() 的方程为
的方程为 ![]() .
.
由 ![]() 得
得 ![]() ,
,
所以 ![]() 或
或 ![]() ,得
,得 ![]() .
.
因为 ![]() ,所以
,所以 ![]() ,于是
,于是 ![]() ,
,
即 ![]()
![]()
![]() ,所以
,所以 ![]() .
.
所以直线AB的斜率为 ![]() .
.
法二:由(1)可知,椭圆方程为 ![]() ,则
,则 ![]() .
.
设 ![]() ,
, ![]() .
.
由 ![]() ,得
,得 ![]() ,
,
所以 ![]() ,
, ![]() .
.
因为点B,点C都在椭圆 ![]() 上,
上,
所以 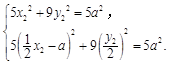
解得 ![]() ,
, ![]() ,
,
所以直线AB的斜率 ![]() .
.
【解析】(1)将点代入椭圆,结合a,b,c的关系即可求出a,b。(2)设出B,C点,由 ![]() 向量关系得到点B、C间坐标关系,再将点B或C代入椭圆解出B或C点,即可求出斜率。
向量关系得到点B、C间坐标关系,再将点B或C代入椭圆解出B或C点,即可求出斜率。

练习册系列答案
相关题目