题目内容
设i是虚数单位，
（1+i）=3-i，则复数Z=（ ）
. |
| Z |
| A、1+2i | B、1-2i |
| C、2+i | D、2-i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由
（1+i）=3-i求出
，再根据共轭复数的概念求解．
. |
| Z |
. |
| Z |
解答：
解：由
（1+i）=3-i，得
（1+i）（1-i）=（3-i）（1-i），2
=2-4i，
∴
=1-2i
∴z=1+2i，
故选：A．
. |
| Z |
. |
| Z |
. |
| Z |
∴
. |
| Z |
∴z=1+2i，
故选：A．
点评：本题考查了复数代数形式的基本运算，复数共轭复数的概念．属于基础题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
复数z=
（i为虚数单位），则z的共轭复数
为（ ）
| 2 |
| 1-i |
. |
| z |
| A、1-i | B、1+i |
| C、3-i | D、3+i |
已知三棱锥的三视图如图所示，则它的体积为（ ）
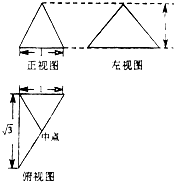
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数x，y满足条件
，则y-（
）x的最大值为（ ）
|
| 1 |
| 2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、1 |
设曲线C的参数方程为
（t为参数），若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为（ ）
|
| A、sinθ=ρcos2θ |
| B、sinθ=ρcosθ |
| C、2sinθ=ρcos2θ |
| D、sinθ=2ρcos2θ |
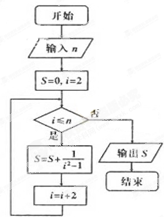
如图所示的程序框图，则输出的结果为（ ）
| A、189 | B、381 |
| C、93 | D、45 |
函数f（x）=sinx（x∈[0，π]），在区间[0，π]上任取一点x0，则f（x0）≥
的概率为（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
