题目内容
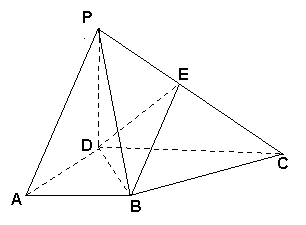
如图,四棱锥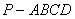 中,底面
中,底面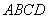 为梯形,
为梯形, ∥
∥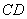 ,
, 

 ,
,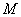 为
为 的中点
的中点
(1)证明:
(2)若 ,求二面角
,求二面角 的余弦值
的余弦值
)解:(Ⅰ)由余弦定理得BD=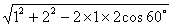 =
=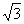
 ∴BD2+AB2=AD2
∴BD2+AB2=AD2
∴∠ABD=90°,BD⊥AB
∵AB∥DC, ∴BD⊥DC
∵PD⊥底面ABCD,BDÌ底面ABCD
∴BD⊥PD
又∵PD∩DC=D, ∴BD⊥平面PDC,
又∵PCÌ平面PDC, ∴BD⊥PC (6分)
(Ⅱ)已知AB=1,AD=CD=2,PD=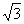 ,
,
由(Ⅰ)可知BD⊥平面PDC.
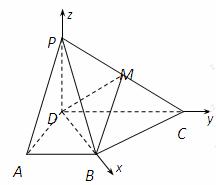
如图,以D为坐标原点,射线DB为x轴的正半轴建立空间直角坐标系D—xyz,则
D(0,0,0),B(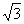 ,0,0),C(0,2,0),P(0,0,
,0,0),C(0,2,0),P(0,0,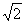 ),M(0,1,
),M(0,1,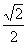 ).
).
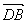 =(
=(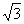 ,0,0),
,0,0),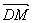 =(0,1,
=(0,1,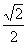 ),
),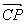 =(0,-2,
=(0,-2,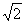 ),
),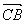 =(
=(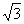 ,-2,0) (7分)
,-2,0) (7分)
设平面BDM的法向量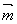 =(x,y,z),则
=(x,y,z),则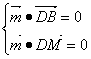
x=0,y+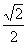 z=0,令z=
z=0,令z=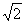 , ∴取
, ∴取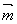 =(0,-1,
=(0,-1,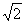 ) (8分)
) (8分)
同理设平面BPM的法向量为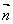 =(a,b,c),则
=(a,b,c),则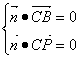
∴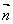 =(
=(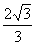 ,1,
,1,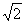 ) (10分)
) (10分)
∴cos<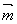 ,
,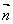 > =
> =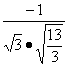 =-
=-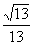 (11分)
(11分)
∴二面角D-BM-P的余弦值大小为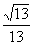 . (12分)
. (12分)

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目

 展开式中
展开式中 的系数是________.
的系数是________.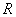 上可导的任意函数
上可导的任意函数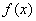 ,若满足
,若满足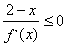 ,则必有
,则必有 B.
B. 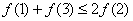
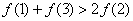 D.
D. 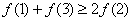
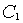 的参数方程为
的参数方程为 ;在极坐标系(以原点为坐标原点,以轴正半轴为极轴)中曲线
;在极坐标系(以原点为坐标原点,以轴正半轴为极轴)中曲线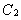 的方程为
的方程为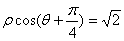 ,则
,则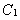 与
与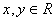 ”,若x
”,若x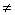 2或y
2或y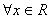 ,ex﹥0”的否定是:“
,ex﹥0”的否定是:“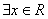 ,ex﹥0”。
,ex﹥0”。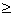 g(x)max。
g(x)max。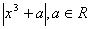 在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-
在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-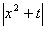 有4个零点,则实数t的取值范围为。
有4个零点,则实数t的取值范围为。 ) B. (
) B. (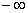 1, -1) C. (
1, -1) C. (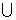 (1,
(1, 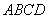 中,
中,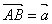 ,
, ,
,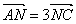 ,
,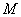 为
为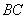 的中点,则
的中点,则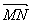 =( )
=( ) B.
B. C.
C.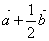 D.
D.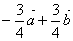
 上存在不同的三点到原点的距离构成等比数列,则该公比不可能是( )
上存在不同的三点到原点的距离构成等比数列,则该公比不可能是( ) B.
B. C.
C. D.
D.