题目内容
11.在公差为d的等差数列{an}中,已知a1=10且5a3•a1=(2a2+2)2.(1)求d,an.
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
分析 (1)由题意可得d的方程,解方程可得通项公式;
(2)易得数列的前10项为正数,第11项为0,从第12项开始为负数,当n≤11时,|a1|+|a2|+|a3|+…+|an|=a1+a2+a3+…+an;当n≥12时,|a1|+|a2|+|a3|+…+|an|=a1+a2+a3+…a11-a12-an=-(a1+a2+a3+…+an)+2(a1+a2+a3+…a11),分别由等差数列的求和公式可得.
解答 解:(1)∵在公差为d的等差数列{an}中a1=10且5a3•a1=(2a2+2)2,
∴5(10+2d)•10=4(11+d)2,整理可得d2-3d-4=0,解得d=4或d=-1,
当d=4时,an=10+4(n-1)=4n+6;
当d=-1时,an=10-(n-1)=-n+11;
(2)由(1)可得d<0时,an=-n+11,
∴数列的前10项为正数,第11项为0,从第12项开始为负数,
∴当n≤11时,|a1|+|a2|+|a3|+…+|an|=a1+a2+a3+…+an=$\frac{(10-n+11)n}{2}$=-$\frac{1}{2}$n2+$\frac{21}{2}$n;
当n≥12时,|a1|+|a2|+|a3|+…+|an|=a1+a2+a3+…a11-a12-an
=-(a1+a2+a3+…+an)+2(a1+a2+a3+…a11)
=$\frac{1}{2}$n2-$\frac{21}{2}$n+2(-$\frac{1}{2}$×112+$\frac{21}{2}$×11)
=$\frac{1}{2}$n2-$\frac{21}{2}$n+110
点评 本题考查等差数列的求和公式和通项公式,涉及分类讨论的思想,属中档题.

练习册系列答案
相关题目
2.复数z=2-4i在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.已知命题p:?x∈(0,$\frac{π}{2}$),x>sinx;命题q:?x∈(0,$\frac{π}{2}$),sinx+cosx=$\frac{9}{10}$,下列命题为真命题的是( )
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
20.已知函数f(x)=|$\left\{\begin{array}{l}{|\frac{lnx}{x}|,0<x≤e}\\{-\frac{1}{2{e}^{2}}x+\frac{3}{2e},x>e}\end{array}\right.$,若a<b<c,且f(a)=f(b)=f(c),则$\frac{blna}{alnb}$•c的取值范围为( )
| A. | (e,3e) | B. | (-3e,-e) | C. | (1,3e) | D. | (-3e,-1) |
1.64是等比数列1,2,4,8…的( )
| A. | 第6项 | B. | 第7项 | C. | 第8项 | D. | 第9项 |
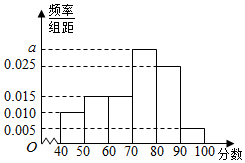 某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).
某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).