题目内容
3．
如图，两条异面直线a，b所成的角为θ，在直线a，b上分别取点A′，E和点A，F，使AA′⊥a，且AA′⊥b（AA′称为异面直线a，b的公垂线），已知A′E=m，AF=n，EF=l，求公垂线AA′的长．
分析 由题意，$\overrightarrow{EF}$=$\overrightarrow{EA′}$+$\overrightarrow{A′A}$+$\overrightarrow{AF}$，两边平方，结合条件，即可求公垂线AA′的长．
解答 解：由题意，$\overrightarrow{EF}$=$\overrightarrow{EA′}$+$\overrightarrow{A′A}$+$\overrightarrow{AF}$，
∴${\overrightarrow{EF}}^{2}$=$\overrightarrow{EA′}$2+$\overrightarrow{A′A}$2+$\overrightarrow{AF}$2+2$\overrightarrow{EA′}$•$\overrightarrow{A′A}$+2$\overrightarrow{AA′}$•$\overrightarrow{AF}$+2$\overrightarrow{EA′}$•$\overrightarrow{AF}$，
∴l2=m2+$\overrightarrow{A′A}$2+n2±2mncosθ，
∴|$\overrightarrow{A′A}$|=$\sqrt{{l}^{2}-{m}^{2}-{n}^{2}±2mncosθ}$．
点评 本题考查求公垂线AA′的长，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
18．如图，半径为R的球O中有一内接圆柱，当圆柱的侧面积最大时，球的体积与该圆柱的体积之比是（ ）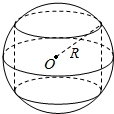
| A． | $\frac{4}{3}$ | B． | $\frac{4\sqrt{2}}{3}$ | C． | $\sqrt{2}$ | D． | $\frac{\sqrt{2}}{3}$ |