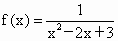题目内容
已知
。
(1)求证f(x)是定义域内的增函数；
(2)求f(x)的值域．
。(1)求证f(x)是定义域内的增函数；
(2)求f(x)的值域．
（1）证明：f(x)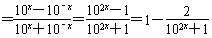
，
令x2＞x1，
则f(x2)-f(x1)=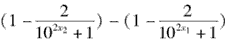
，
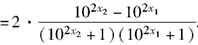∵10x为增函数，
∴当x2＞x1时，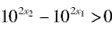
，
又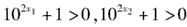
，
故当x2＞x1时，f(x2)-f(x1)＞0，即f(x2)＞f(x1)，
所以f(x)是增函数．
（2）解：令y=f(x)，由y=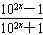
，解得102x=
，
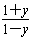∵102x＞0，
∴-1＜y＜1，
即f(x)的值域为(-1，1)．
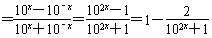，令x2＞x1，
则f(x2)-f(x1)=
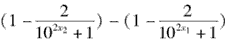
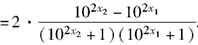，∵10x为增函数，
∴当x2＞x1时，
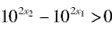，又
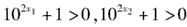，故当x2＞x1时，f(x2)-f(x1)＞0，即f(x2)＞f(x1)，
所以f(x)是增函数．
（2）解：令y=f(x)，由y=
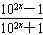，解得102x=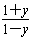，∵102x＞0，
∴-1＜y＜1，
即f(x)的值域为(-1，1)．
练习册系列答案
相关题目
；
，求数列{an}的通项公式；
，求证：对一切
，
．
．