题目内容
如图,正三棱锥O-ABC的三条侧棱OA、OB、OC两两垂直,且长度均为2.E、F分别是AB、AC的中点,H是EF的中点,过EF作平面与侧棱OA、OB、OC或其延长线分别相交于A1、B1、C1,已知![]() .
.

(1)求证:B1C1⊥平面OAH;
(2)求二面角O-A1B1-C1的大小;
答案:
解析:
解析:
|
解:(1)证明:依题设, 又 因为 所以 因此 (2)作 作 设 在 所以
解法二:(1)以直线 所以 所以 所以 由 (2)由已知 则 由 同理: 设 则 又 所以二面角的大小为
(3)由(2)知, 则 则点 |

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
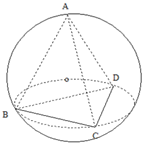 如图,正三棱锥ABCD内接于球O,底面边长为
如图,正三棱锥ABCD内接于球O,底面边长为| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|


 令
令



 ,侧棱长为2,则球O的表面积为( )
,侧棱长为2,则球O的表面积为( )




 ,侧棱长为2,则球O的表面积为( )
,侧棱长为2,则球O的表面积为( )



