题目内容
设双曲线x2-y2=6的左右顶点分别为A1、A2,P为双曲线右支上一点,且位于第一象限,直线PA1、PA2的斜率分别为k1、k2,则k1•k2的值为________.
1
分析:设点P(x0,y0),则点P的坐标满足双曲线的方程 .利用双曲线x2-y2=6的方程即可得到顶点A1、A2的坐标,利用斜率计算公式即可得到直线PA1、PA2的斜率并相乘得k1•k2=
.利用双曲线x2-y2=6的方程即可得到顶点A1、A2的坐标,利用斜率计算公式即可得到直线PA1、PA2的斜率并相乘得k1•k2= 即可证明.
即可证明.
解答:设点P(x0,y0),则 .
.
由双曲线x2-y2=6得a2=6,解得 .
.
∴ ,
, .
.
∴k1•k2= =
= =1.
=1.
故答案为1.
点评:熟练掌握双曲线的方程及其性质、斜率计算公式是解题的关键.
分析:设点P(x0,y0),则点P的坐标满足双曲线的方程
 .利用双曲线x2-y2=6的方程即可得到顶点A1、A2的坐标,利用斜率计算公式即可得到直线PA1、PA2的斜率并相乘得k1•k2=
.利用双曲线x2-y2=6的方程即可得到顶点A1、A2的坐标,利用斜率计算公式即可得到直线PA1、PA2的斜率并相乘得k1•k2= 即可证明.
即可证明.解答:设点P(x0,y0),则
 .
.由双曲线x2-y2=6得a2=6,解得
 .
.∴
 ,
, .
.∴k1•k2=
 =
= =1.
=1.故答案为1.
点评:熟练掌握双曲线的方程及其性质、斜率计算公式是解题的关键.

练习册系列答案
相关题目
设双曲线x2-y2=1的两条渐近线与直线x=
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数z=3x-2y的取值范围为( )
| ||
| 2 |
A、[0,
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[0,
|
 围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数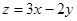 的取值范围为( )
的取值范围为( )  ]
B.[
]
B.[ ] C.[
] C.[ ] D.
[
] D.
[ ]
]