题目内容
设双曲线x2-y2=1的两条渐近线与直线x=
| ||
| 2 |
分析:求出双曲线x2-y2=1的两条渐近线方程,然后把这两个方程和直线x=
构成三个方程组,解这三个方程组的解,得到三角形三个顶点的坐标,把这三个顶点坐标分别代入目标函数z=x-2y得到三个值,其中最小的就是目标函数z=x-2y的最小值.
| ||
| 2 |
解答:解:双曲线x2-y2=1的两条渐近线是y=±x,解方程组
,
,,
得到三角形区域的顶点坐标是A(
,
),B(
,-
),C(0,0).∴zA=
-2×
=-
,zB=
-2× (-
)=
,zC=0.
∴目标函数z=x-2y的最小值为-
.
答案:-
.
|
|
|
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴目标函数z=x-2y的最小值为-
| ||
| 2 |
答案:-
| ||
| 2 |
点评:把三角形区域三个顶点坐标分别代入目标函数z=x-2y得到三个值,其中最小的就是目标函数z=x-2y的最小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设双曲线x2-y2=1的两条渐近线与直线x=
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数z=3x-2y的取值范围为( )
| ||
| 2 |
A、[0,
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[0,
|
 围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数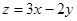 的取值范围为( )
的取值范围为( )  ]
B.[
]
B.[ ] C.[
] C.[ ] D.
[
] D.
[ ]
]