题目内容
设双曲线x2-y2=1的两条渐近线与直线x=
围成的三角形区域(包含边界)为D,点P(x,y)为D内的一个动点,则目标函数z=x-2y的最小值为( )
| ||
| 2 |
| A、-2 | ||||
B、-
| ||||
| C、0 | ||||
D、
|
分析:依题意可知平面区域是由y=x,y=-x,x=
构成.把可行域三角形的三个顶点坐标代入z即可求得最小值.
| ||
| 2 |
解答:解:依题意可知平面区域是由y=x,y=-x,x=
构成.
可行域三角形的三个顶点坐标为(0,0),(
,
),(
,-
),
将这三点代可求得Z的最小值为-
.
故选B
| ||
| 2 |
可行域三角形的三个顶点坐标为(0,0),(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
将这三点代可求得Z的最小值为-
| ||
| 2 |
故选B
点评:本题主要考查了双曲线的简单性质和简单线性规划问题.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设双曲线x2-y2=1的两条渐近线与直线x=
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数z=3x-2y的取值范围为( )
| ||
| 2 |
A、[0,
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[0,
|
 围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数
围成的三角形区域(包含边界)为E,P(x,y)为该区域内的一个动点,则目标函数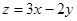 的取值范围为( )
的取值范围为( )  ]
B.[
]
B.[ ] C.[
] C.[ ] D.
[
] D.
[ ]
]