题目内容

解:(Ⅰ)当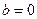 时,
时,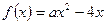 ,
,
若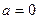 ,
,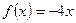 ,则
,则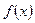 在
在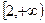 上单调递减,不符题意。---2分
上单调递减,不符题意。---2分
故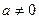 ,要使
,要使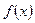 在
在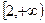 上
上 单调
单调 递增,必须
递增,必须 满足
满足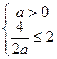 ,∴
,∴ 。---6分
。---6分
(Ⅱ)若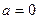 ,
,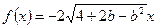 ,则
,则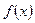 无最大值,故
无最大值,故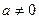 ,∴
,∴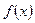 为二次函数,
为二次函数,
要使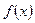 有最大值,必须满足
有最大值,必须满足 ,即
,即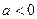 且
且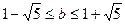 ,
,
此时,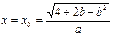 时,
时,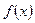 有最大值。----8分
有最大值。----8分
又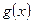 取最小值时,
取最小值时, ,依题意,有
,依题意,有 ,----10分
,----10分
则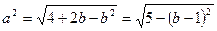 ,
,
∵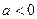 且
且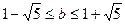 ,∴
,∴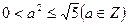 ,得
,得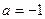 ,此时
,此时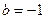 或
或 。
。
∴满足条件的实数对 是
是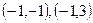 。
。
解析

练习册系列答案
相关题目
题目内容

解:(Ⅰ)当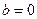 时,
时,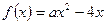 ,
,
若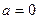 ,
,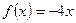 ,则
,则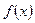 在
在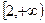 上单调递减,不符题意。---2分
上单调递减,不符题意。---2分
故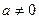 ,要使
,要使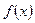 在
在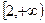 上
上 单调
单调 递增,必须
递增,必须 满足
满足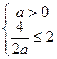 ,∴
,∴ 。---6分
。---6分
(Ⅱ)若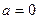 ,
,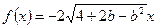 ,则
,则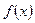 无最大值,故
无最大值,故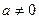 ,∴
,∴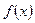 为二次函数,
为二次函数,
要使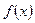 有最大值,必须满足
有最大值,必须满足 ,即
,即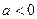 且
且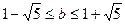 ,
,
此时,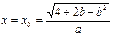 时,
时,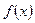 有最大值。----8分
有最大值。----8分
又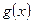 取最小值时,
取最小值时, ,依题意,有
,依题意,有 ,----10分
,----10分
则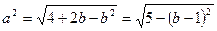 ,
,
∵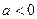 且
且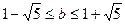 ,∴
,∴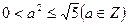 ,得
,得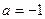 ,此时
,此时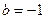 或
或 。
。
∴满足条件的实数对 是
是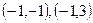 。
。
解析
