题目内容
(本小题满分14分)
已知函数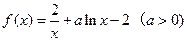 .
.
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线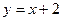 垂直,求函数
垂直,求函数 的单调区间;
的单调区间;
(2)若对于 都有
都有 成立,试求
成立,试求 的取值范围;
的取值范围;
(3)记 .当
.当 时,函数
时,函数 在区间
在区间 上有两个零点,
上有两个零点,
解:(I) 直线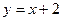 的斜率为1.函数
的斜率为1.函数 的定义域为
的定义域为 ,
, ,所以
,所以 ,所以
,所以 . 所以
. 所以 .
.  .由
.由 解得
解得 ;[来源:Z,xx,k.Com]
;[来源:Z,xx,k.Com] 由
由 解得
解得 .
.
所以 的单调增区间是
的单调增区间是 ,单调减区间是
,单调减区间是 . ……………………4分
. ……………………4分
(II) ,由
,由 解得
解得 ;由
;由 解得
解得 .
.
所以 在区间
在区间 上
上 单调递增,在区
单调递增,在区 间
间 上单调递减.
上单调递减.
所以当 时,函数
时,函数 取得最小值,
取得最小值, .
.
因为对于 都有
都有 成立,所以
成立,所以 即可.
即可.
则 . 由
. 由 解得
解得 . 所以
. 所以 的范围
的范围 是
是 .……9分
.……9分
(III)依题得 ,则
,则 .由
.由 解得
解得 ;由
;由 解得
解得
 .
.
所以函数 在区间
在区间 为减函数,在区间
为减函数,在区间 为增函数.
为增函数.
又因为函数 在区间
在区间 上有两个零点,所以
上有两个零点,所以
解得 .所以
.所以 的取值范围是
的取值范围是 . …………14分
. …………14分
解析

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 ,(
,( 为常数)
为常数) 时,求函数的单调区间;
时,求函数的单调区间;  有两个极值点,求实数
有两个极值点,求实数 ,其中
,其中 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 上,
上, 恒成立,求a的取值范围.
恒成立,求a的取值范围. .
. 在
在 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围;
的取值范围; 时,
时, 上的最小值为
上的最小值为 ,求
,求 与曲线
与曲线 交于点
交于点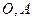 .直线
.直线 与曲线
与曲线 分别相交于点
分别相交于点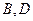 .
. 的面
的面 积
积 与
与 的函数关系
的函数关系 ;
; 的单调性,并求
的单调性,并求

 ,曲线在点M处的切线恰好与直线
,曲线在点M处的切线恰好与直线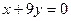 垂直
垂直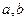 的值
的值 )若函数
)若函数 的取值范围。
的取值范围。 设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
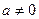 时,求:函数
时,求:函数 的单调区间;
的单调区间; 时,求证:当
时,求证:当 时,不等式
时,不等式