题目内容
周长为a的扇形,圆心角等于分析:设扇形的半径为r,弧长为l,利用周长关系,表示出扇形的面积,利用二次函数求出面积的最大值,以及圆心角的大小.
解答:解:设扇形的半径为r,弧长为l,则
l+2r=a,即l=a-2r(0<r<
).
扇形的面积S=
lr,将上式代入,
得S=
(a-2r)r=-r2+
ar=-(r-
a)2+
,
所以当且仅当r=
a时,S有最大值
,
此时l=
,
所以α=
=2rad.
所以当α=2rad时,扇形的面积取最大值,最大值
.
l+2r=a,即l=a-2r(0<r<
| a |
| 2 |
扇形的面积S=
| 1 |
| 2 |
得S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| a2 |
| 4 |
所以当且仅当r=
| 1 |
| 4 |
| a2 |
| 4 |
此时l=
| a |
| 2 |
所以α=
| l |
| r |
所以当α=2rad时,扇形的面积取最大值,最大值
| a2 |
| 4 |
点评:本题是基础题,考查扇形的周长,半径圆心角,面积之间的关系,考查计算能力.

练习册系列答案
相关题目
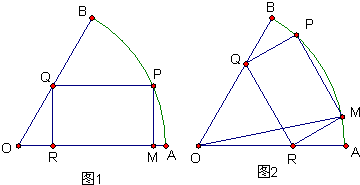
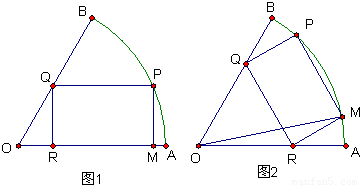
 半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)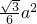 ,那么请问哪种裁法能得到最大面积的矩形?说明理由.
,那么请问哪种裁法能得到最大面积的矩形?说明理由.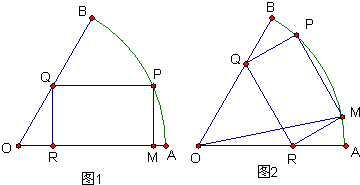
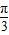 半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)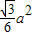 ,那么请问哪种裁法能得到最大面积的矩形?说明理由.
,那么请问哪种裁法能得到最大面积的矩形?说明理由.