题目内容
12.设集合A={x|y=lg(x-2)},集合B={x|y=$\sqrt{3-x}$},则A∩B=( )| A. | {x|x<2} | B. | {x|x≤2} | C. | {x|2<x≤3} | D. | {x|2≤x<3} |
分析 分别解关于A、B的不等式,求出A、B的交集即可.
解答 解:∵A={x|y=lg(x-2)}={x|x>2},
B={x|y=$\sqrt{3-x}$}={x|x≤3},
则A∩B=(2,3],
故选:C.
点评 本题考查了集合的运算,考查对数函数以及二次根式的性质,是一道基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
2.为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6根弹簧进行测量,得到如下数据:
(1)画出散点图;
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归方程.
( 其中 $\begin{array}{l}b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\\ a=\overline y-b\overline x\end{array}$)
| x (g) | 5 | 10 | 15 | 20 | 25 | 30 |
| y (cm) | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归方程.
( 其中 $\begin{array}{l}b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\\ a=\overline y-b\overline x\end{array}$)
7.某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
(1)判断是否在犯错误的概率不超过0.5%的前提下认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| 喜欢 | 不喜欢 | 总计 | |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 总计 | 30 | 25 | 55 |
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17.已知等差数列{an}的前n项和为Sn,设A(a1009,1),B(2,-1),C(2,2)为坐标平面上三点,O为坐标原点,若向量$\overrightarrow{OA}$与$\overrightarrow{OB}$在向量$\overrightarrow{OC}$方向上的投影相同,则S2017为( )
| A. | -2016 | B. | -2017 | C. | 2017 | D. | 0 |
4.在等差数列{an}中,a10=$\frac{1}{2}$a14-6,则数列{an}的前11项和等于( )
| A. | 132 | B. | 66 | C. | -132 | D. | -66 |
1.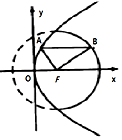 如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
 如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )| A. | (6,10) | B. | (8,12) | C. | [6,8] | D. | [8,12] |