题目内容
13.数列{xn},{yn}定义如下:x1=1,y1=39,且xn+1=23xn+yn+2,yn+1=551xn+24yn+64,n=1,2…证明:对一切正整数n,xn是完全平方数.
分析 由已知24xn+1=24×23xn+24yn+48,yn+1=551xn+24yn+64,两式相减,得:xn+2=47xn+1-xn+18,从而xn+3=48xn+2-48xn+1+xn,设${a}_{n}=\sqrt{{x}_{n}}$,则${{a}_{n+3}}^{2}=48{{a}_{n+2}}^{2}-48{{a}_{n+1}}^{2}+{{a}_{n}}^{2}$,再证明{an}是正整数数列,由此能证明对于一切正整数n,xn是完全平方数.
解答 证明:∵数列{xn},{yn}定义如下:x1=1,y1=39,
且xn+1=23xn+yn+2,yn+1=551xn+24yn+64,n=1,2…
∴24xn+1=24×23xn+24yn+48,yn+1=551xn+24yn+64,
两式相减,得:24xn+1=yn+1+xn-16,又xn+2=23xn+1+yn+1+2,
消去yn+1,得:xn+2=47xn+1-xn+18,
∴xn+3=47xn+2-xn+1+18,
两式相减,得:xn+3=48xn+2-48xn+1+xn,
由x1=1,y1=39,得x2=64,y2=3025,
设${a}_{n}=\sqrt{{x}_{n}}$,则a1=1,a2=8,a3=55,且${{a}_{n+3}}^{2}=48{{a}_{n+2}}^{2}-48{{a}_{n+1}}^{2}+{{a}_{n}}^{2}$,①
下面证明{an}是正整数数列,
由①得:${{a}_{n+3}}^{2}-(49{{a}_{n+2}}^{2}-14{a}_{n+2}{a}_{n+3}+{{a}_{n+1}}^{2})$=${{a}_{n}}^{2}-(49{{a}_{n+1}}^{2}-14{a}_{n+1}{a}_{n+2}+{{a}_{n+2}}^{2})$,
∴(an+3+an+1-7an+2)(an+3+7an+2-an+1)=(an+2+an-7an+1)(an+3+7an+1-an+2).
∵${a}_{3}+{a}_{1}-7{a}_{2}=\sqrt{3025}+\sqrt{1}-7\sqrt{64}$=0,∴(an+3+an+1-7an+2)(an+3+7an+2-an+1)=0,
∵{xn}是严格单调增函数,∴{an}也是严格单调增函数,
∴an+3+7an+2-an+1>0,
∴an+3+an+1-7an+2=0,即an+3=7an+2-an+1,a1=1,a2=8,
∴{an}是正整数数列,
从而对于一切正整数n,xn是完全平方数.
点评 本题考查对一切正整数n,xn是完全平方数的证明,综合性强,难度大,对数学思维的要求较高,解题时要认真审题,注意函数的单调性、数列的性质的合理运用.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案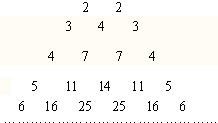 如图,它满足(1)第n行首尾两数均为n,
如图,它满足(1)第n行首尾两数均为n,