题目内容
14.画出满足下列极坐标方程的曲线的图象:(1)ρcosθ=1;(2)ρ=6cosθ;
(3)ρ=10sinθ;(4)ρ=10(1+cosθ)
分析 再利用角坐标与极坐标间的关系化成直角坐标方程即可.
解答 解:(1)由ρcosθ=1,得:x=1,如图示: ,
,
(2)ρ=6cosθ;
ρ2=6ρcosθ
x2+y2=6x,即(x-3)2+y2=9,
表示圆,如图示: ;
;
(3)ρ=10sinθ
ρ2=10ρsinθ
x2+y2=10y,即x2+(y-5)2=25,
表示圆,如图示: ;
;
(4)ρ2=10ρ+10ρ•cosθ,
x2+y2=10$\sqrt{{x}^{2}{+y}^{2}}$+10x
x2+y2-10x-10$\sqrt{{x}^{2}{+y}^{2}}$=0,
如图示: .
.
点评 本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
相关题目
4.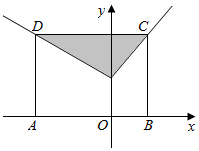 如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
 如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
2.从1,2,3,4,5,6,7这七个数字中任取两个数字相加,其和为偶数的概率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
9.营养师要为儿童预定午餐和晚餐,已知一个单位的午餐含12个单位的碳税化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含有8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C,另外,这两餐需要的营养中至少含有64个单位的碳水化合物,42个单位的蛋白质和54个维生素C.
(Ⅰ)根据已知数据填写如表:
(Ⅱ)已知一个单位的午餐,晚餐的费用分别是4元和5元,若预定x个单位的午餐和y个单位的晚餐,共花费z元,请列出满足上述营养要求的不等式组及目标函数;
(Ⅲ)在(Ⅱ)的条件下,并且花费最少,应分别预定多少个单位的午餐和晚餐?
(Ⅰ)根据已知数据填写如表:
| 营养成分 | 碳水化合物/单位 | 蛋白质/单位 | 维生素C/单位 |
| 午餐 | |||
| 晚餐 |
(Ⅲ)在(Ⅱ)的条件下,并且花费最少,应分别预定多少个单位的午餐和晚餐?