题目内容

已知函数
(I)求不等式的解集;
(II)设，若关于的不等式的解集非空，求实数的取值范围.

(Ⅰ)原不等式的解为 ；(Ⅱ) .

解析试题分析：(Ⅰ)原不等式可化为： 即：2分
由得      由得
综上原不等式的解为     5分
(Ⅱ)原不等式等价于
令，即，    8分
由，所以，
所以.      10分
考点：本题主要考查简单绝对值不等式的解法，绝对值的几何意义。
点评：中档题，解简单绝对值不等式，一般要考虑去绝对值的符号。有时利用绝对值的几何意义则更为简单。（II）转化成的解集非空后，通过构造函数，确定函数的最小值，使问题得解。

练习册系列答案
相关题目
已知函数f（x）满足f(x)=x3+f′(
2
3
)x2-x+c（其中f′(
2
3
)为f（x）在点x=
2
3
的导数，C为常数）
（I）若方程f（x）=0有且只有两个不等的实根，求常数C；
（II）在（I）的条件下，若f(-
1
3
)＞0，求函数f（x）的图象与X轴围成的封闭图形的面积．
已知函数f（x）=e-x（2x-a），a∈R．
（I）讨论函数f（x）的单调性；
（II）若关于实数x的方程f（x）=1在[
12
，2]上有两个不等实根，求a的取值范围．
（2013•绵阳二模）已知函数f（x）=xlnx（x∈（0，+∞）
（I ）求g（x）=
f(x+1)
x+1
-x(x∈(-1，+∞))的单调区间与极大值；
（II ）任取两个不等的正数x1，x2，且x1＜x2，若存在x0＞0使f′（x0）=
f(x2)-f(x1)
x2-x1
成立，求证：x1＜x0＜x2
（III）己知数列{an}满足a1=1，an+1=（1+
1
2n
）an+
1
n2
（n∈N+），求证：an＜e
11
4
（e为自然对数的底数）．
已知函数f（x）满足f（x）=x3+f′（
2
3
）x2-x+c（其中c为常数）
（I）若方程f（x）=0有且只有两个不等的实根，求常数c；
（II）在（I）的条件下，若f（-
1
3
）＞0，求函数f（x）的图象与x轴围成的封闭图形的面积．

（本题满分12分）已知函数。
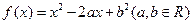（I）若从集合{0，1，2，3}中任取一个元素作为，从集合{0，1，2}中任取一个元素作为b，求方程有两个不等实数根的概率；
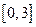（II）若从区间[0，2]中任取一个数作为，从区间中任取一个数作为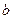，求方程没有实数根的概率。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网